Question

Show that angle of reflection is equal to angle of incidence on the basis of Huygens wave of light with the help of a labelled diagram for the derivation.

Answer 1

The proof for angle of reflection is equal to angle of incidence according to Huygen’s principle differ from the normal proof because we take a light wave as a plane wave front instead of representing it as a single ray. In this we relate angles and sides of triangles and prove similar triangles and hence relate the desired angles.

Complete answer:
According to huygen’s principle, “Various points of an arbitrary surface, when reached by a wavefront, become secondary sources of light emitting secondary wavelets. The disturbance beyond the surface results from the superposition of these secondary wavelets”.
Now, for the proof, let us consider the given diagram. Here, $S{{S}^{'}}$ is a reflecting surface where $AB$, a plane wavefront which is striking at $A$. Let $v$ be the velocity of light and it takes some time $t$to reach from edge$B$to the reflecting surface at point $A'$.
As stated in Huygen's principle, such points on a wave front act as a surface of secondary wavelets. If the surface $S{{S}^{'}}$ is absent, the wavefront $AB$ would have reached $A'D$ which is parallel to $AB$.
So, when we the wavefront $AB$ meet at point $A'$ at time $t$, the secondary wavelet from $A$ will have acquired a radius of $AB'$.
Where, $AB'=BA'=AD=vt$
The incident ray will cover a distance equal to$AB'$ by the time the incident wavefront reaches$A'$.
Now let us consider the triangles formed. From $\vartriangle ABA'$ and $\vartriangle A'B'A$,
$\angle B=\angle B'=90{}^\circ$
$AA'$is common and $AB'=AB'=vt$.
Therefore, those triangles are congruent. So we can relate that,
$\angle BAA'=\angle B'A'A$
i.e., $\angle i=\angle r$
So, we proved that angle of incidence is equal to angle of reflection in case of reflection of a light beam on a surface by considering Huygens principles.

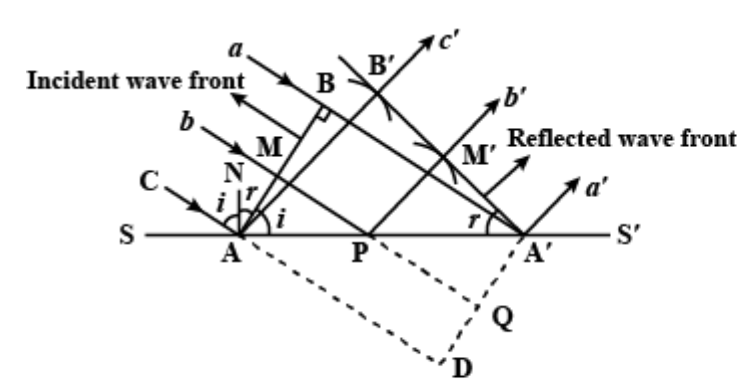
Note: From this diagram itself we can also prove the first law of reflection. As $AB,A'S'$ and $SS'$ are in the same plane. While proving the second law. It is important to remember the distance travelled by one end of the wavefront to reach the surface. The whole idea depends on that point and using it to prove the congruence of triangles formed.