Question

Show that a triangle of maximum area that can be inscribed in a circle of radius $'r'$ is an equilateral triangle.

Answer 1

Here we will first draw a triangle inside the circle and we will draw the height of the triangle. Then we will find the area of that triangle using base and height. We will then differentiate the area and equate it with zero. From there, we will find the sides of the triangle and we will find that the given triangle is an equilateral triangle or not.

Complete step-by-step answer:

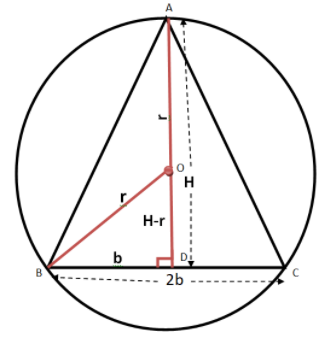
We will first draw the circle and triangle inscribed inside it.
It is given that $r$ is the radius of the given circle.
Let $H$ be the height of the triangle and $2b$ be the base of the triangle.
Let $AD$ be the height of a triangle, so it will be perpendicular to the base $BC$.
We know that the perpendicular from the center bisects the chord.
Therefore,
$BD = CD = b$.
$\Delta OBD$ is a right angled triangle.
Using Pythagoras theorem in $\Delta OBD$, we get
$O{B^2} = O{D^2} + B{D^2}$
Now, we will substitute the value of $OB$, $OD$ and $BD$.
$\Rightarrow {r^2} = {\left( {H - r} \right)^2} + {b^2}$
Applying exponents on the bases, we get
$\Rightarrow {r^2} = {r^2} + {H^2} - 2rH + {b^2}$
On further simplification, we get
$\Rightarrow {b^2} = 2rH - {H^2}$………$$$$ $\left( 1 \right)$
Here, we need to maximize the area of the triangle.
We know area of triangle is $\dfrac{1}{2} \times {\rm{base}} \times {\rm{height}}$
Therefore,
Area of$\Delta ABC = \dfrac{1}{2} \times 2b \times H$
Simplifying the terms, we get
Area of $\Delta ABC = bH$
We have calculated the value of ${b^2}$. But in the value of $b$, we will get a square root which is difficult to differentiate. So we will square the area of $\Delta ABC$ and assume the value to be $Z$.
So,
$Z = {\rm{Are}}{{\rm{a}}^2}$
Putting the value area, we get
$\begin{array}{l} \Rightarrow Z = {\left( {b \times H} \right)^2}\\\ \Rightarrow Z = {b^2} \times {H^2}\end{array}$
Substituting the value of ${b^2}$from equation $\left( 1 \right)$, we get
$\Rightarrow Z = \left( {2rH - {H^2}} \right) \times {H^2}$
Multiplying the terms, we get
$\Rightarrow Z = 2r{H^3} - {H^4}$
Differentiating $Z$ with respect to $H$, we get
$\begin{array}{l} \Rightarrow \dfrac{{dZ}}{{dH}} = \dfrac{{d\left( {2r{H^3} - {H^4}} \right)}}{{dH}}\\\ \Rightarrow \dfrac{{dZ}}{{dH}} = 6r{H^2} - 4{H^3}\end{array}$
Now, we will equate $\dfrac{{dZ}}{{dH}}$ with zero.
Therefore,
$\Rightarrow 6r{H^2} - 4{H^3} = 0$
Factoring the above equation, we get
$\Rightarrow 2{H^2}\left( {3r - 2H} \right) = 0$
Here $H \ne 0$.
$\therefore 3r-2H=0$
On further simplification, we get
$H = \dfrac{{3r}}{2}$………$\left( 2 \right)$
We will again differentiate $\dfrac{{dZ}}{{dH}}$ with respect to$H$.
$\begin{array}{l}\dfrac{d}{{dH}}\left( {\dfrac{{dZ}}{{dH}}} \right) = \dfrac{d}{{dH}}\left( {6r{H^2} - 4{H^3}} \right)\\\ \Rightarrow \dfrac{{{d^2}Z}}{{d{H^2}}} = 12rH - 12{H^2}\end{array}$
Substituting the value of $H$ in the above equation, we get
$\Rightarrow \dfrac{{{d^2}Z}}{{d{H^2}}} = 12r \times \dfrac{{3r}}{2} - 12 \times {\left( {\dfrac{{3r}}{2}} \right)^2}$
Multiplying the terms, we get
$\begin{array}{l} \Rightarrow \dfrac{{{d^2}Z}}{{d{H^2}}} = 18{r^2} - 27{r^2}\\\ \Rightarrow \dfrac{{{d^2}Z}}{{d{H^2}}} = - 9{r^2} < 0\end{array}$
Therefore, $Z$ is maximum when $H = \dfrac{{3r}}{2}$
We will substitute the value of $H$ in equation $\left( 1 \right)$, we get
${b^2} = 2r \times \dfrac{{3r}}{2} - {\left( {\dfrac{{3r}}{2}} \right)^2}$
Multiplying the terms, we get
$\begin{array}{l} \Rightarrow {b^2} = 3{r^2} - \dfrac{{9{r^2}}}{4}\\\ \Rightarrow {b^2} = \dfrac{{3{r^2}}}{4}\end{array}$
Taking square roots on both sides, we get
$\Rightarrow b = \dfrac{{\sqrt 3 r}}{2}$
Therefore,
$BC = 2 \times b = 2 \times \dfrac{{\sqrt 3 r}}{2} = \sqrt 3 r$
Applying Pythagoras theorem in right angled triangle$ABD$, we get
$\begin{array}{l}A{B^2} = B{D^2} + A{D^2}\\\ \Rightarrow A{B^2} = {H^2} + {b^2}\end{array}$
Substituting the values of $H$ and $b$, we get
$\Rightarrow A{B^2} = {\left( {\dfrac{{3r}}{2}} \right)^2} + {\left( {\dfrac{{\sqrt 3 r}}{2}} \right)^2}$
Squaring all the terms, we get
$\Rightarrow A{B^2} = \dfrac{{9{r^2}}}{4} + \dfrac{{3{r^2}}}{4} = 3{r^2}$
Taking square roots on both sides, we get
$\Rightarrow AB = \sqrt 3 r$
Similarly, Applying Pythagoras theorem in right angled triangle$ACD$, we get
$\begin{array}{l}A{C^2} = C{D^2} + A{D^2}\\\ \Rightarrow A{C^2} = {H^2} + {b^2}\end{array}$
Substituting the values of $H$ and $b$, we get
$\Rightarrow A{C^2} = {\left( {\dfrac{{3r}}{2}} \right)^2} + {\left( {\dfrac{{\sqrt 3 r}}{2}} \right)^2}$
Squaring all the terms, we get
$\Rightarrow A{C^2} = \dfrac{{9{r^2}}}{4} + \dfrac{{3{r^2}}}{4} = 3{r^2}$
Taking square roots on both sides, we get
$\Rightarrow AC = \sqrt 3 r$
Hence, we have got $AC = AB = BC = \sqrt 3 {r^2}$.
Thus, $\Delta ABC$ is an equilateral triangle.

Note: The line which passes through the center and perpendicular to the chord, then that line will bisect the chord. We have used Pythagoras theorem here which states that the square of the longest side of the right angled triangle is equal to the sum of the square of the other two sides of a right angled triangle. An equilateral triangle is that triangle whose all the sides are equal and all the angles are $60^\circ$.