Question

Show how you would connect $3$ resistors, each of resistance $6$ ohm so that the combination has a resistance of (i) $9$ ohm (ii) $4$ ohm

Answer 1

Hint
In the given question, we have been provided with three resistances and we can connect them in any possible manner that comes to us, with the condition that the equivalent resistance of the circuit has a certain given value. If the value of the equivalent resistance of the circuit is more than the individual resistance, we can say that the no. of series connection will be more than or equal to the no. of parallel connections, and the inverse situation also stands true.
$\Rightarrow {{\text{R}}_{\text{series}}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+--+{{R}_{n}}$ , $\dfrac{\text{1}}{{{\text{R}}_{\text{parallel}}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+--+\dfrac{1}{{{R}_{n}}}$

Complete step by step answer
Before proceeding ahead, we should establish that
$\Rightarrow {{\text{R}}_{\text{series}}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+--+{{R}_{n}}$ where $\Rightarrow {{\text{R}}_{\text{series}}}$ is the equivalent resistance for series connection
If the resistances have equal values, such as in the question given to us, we can say that
$\Rightarrow {{\text{R}}_{\text{series}}}=nR$ where $n$ is the no. of resistors and $R$ is the value of one resistor
Similarly, we can establish an expression for parallel combination of resistors
$\Rightarrow \dfrac{\text{1}}{{{\text{R}}_{\text{parallel}}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+--+\dfrac{1}{{{R}_{n}}}$
Now if the resistances have equal values, we can say that
$\Rightarrow \dfrac{\text{1}}{{{\text{R}}_{\text{parallel}}}}=\dfrac{n}{R}\Rightarrow {{\text{R}}_{\text{parallel}}}=\dfrac{R}{n}$
In the first case, we have to form a resultant resistance of nine ohm; this equivalent resistance is more than the value of the individual resistance (which is six ohm), so the no. of series connection should be more than or equal to the no. of parallel connections.
If we connect two of the given resistors in series, the resultant would be $(2\times 6\Omega )=12\Omega$
But this is not the requires value, therefore we must now try making one series and one parallel connection as follows

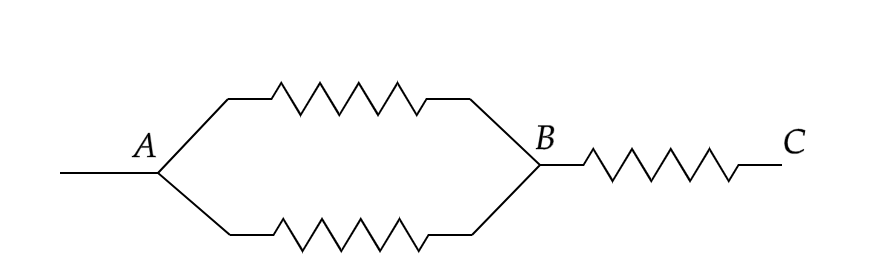
In the above figure, the equivalent resistance of the part AB of the circuit would be $\dfrac{6\Omega }{2}=3\Omega$
The net resistance across AC would hence be $6\Omega +3\Omega =9\Omega$ which is the required net resistance
To answer the second part of the question, the circuit would be as the one given below

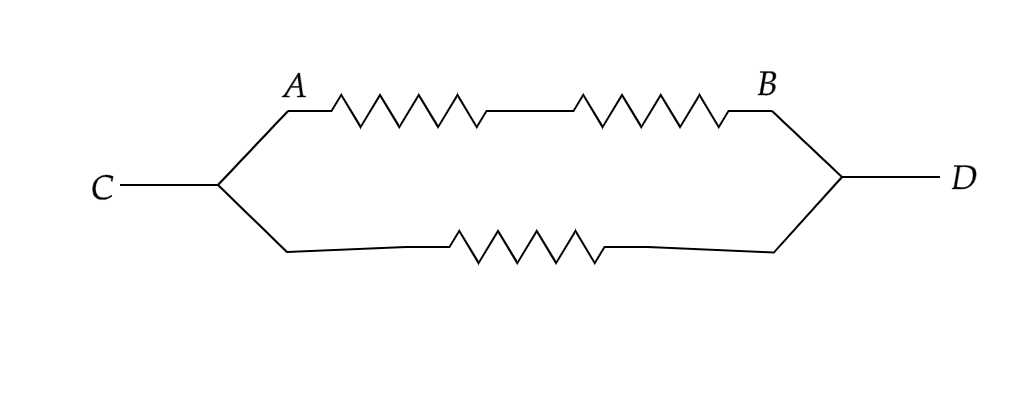
In the above circuit, the resistance of the part AB of the circuit would be $(6+6)\Omega =12\Omega$
Now the arm AB is in parallel with the $6\Omega$ resistance .
The equivalent resistance can now be calculated as -
$\Rightarrow \dfrac{\text{1}}{{{\text{R}}_{\text{parallel}}}}=\dfrac{1}{12}+\dfrac{1}{6}$
$\Rightarrow \dfrac{\text{1}}{{{\text{R}}_{\text{parallel}}}}=\dfrac{3}{12}$
$\Rightarrow {{\text{R}}_{\text{parallel}}}=12/3=4\Omega$
This is the required answer to the second part of our question.

Note
Please refer to the beginning of the solution, where we have established the expression for series and parallel combination of equal resistors if you get confused as to where to multiply and where to divide the resistances. In the second part, we can also use six resistors with three resistors in a parallel combination and two such combinations in series. This question works on a hit and trial method so feel free to make several circuits.