Solveeit Logo
Login

Question

Question: Show by section formula that the points (3, -2), (5, 2) and (8, 8) are collinear....

Show by section formula that the points (3, -2), (5, 2) and (8, 8) are collinear.

Explanation

Solution

  1. The section formula gives the coordinates of a point P(x, y) which divides the line joining two points A(x1,y1)A\left( {{x}_{1}},{{y}_{1}} \right) and B(x2,y2)B\left( {{x}_{2}},{{y}_{2}} \right) in the ratio AP : PB = m : n, internally or externally.
  2. For internal division: P(x,y)=(mx2+nx1m+n,my2+ny1m+n)P(x,y)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right) .
  3. For external division: P(x,y)=(mx2−nx1m−n,my2−ny1m−n)P(x,y)=\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right) .
  4. For three points A(x1,y1)A\left( {{x}_{1}},{{y}_{1}} \right) , B(x2,y2)B\left( {{x}_{2}},{{y}_{2}} \right) and C(x3,y3)C\left( {{x}_{3}},{{y}_{3}} \right) to be collinear, the ratio m : n should be same in both x3=mx2+nx1m+n{{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} and y3=my2+ny1m+n{{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} .
    i.e. mn=x1−x3x3−x2=y1−y3y3−y2\dfrac{m}{n}=\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}} .

Complete step by step solution:
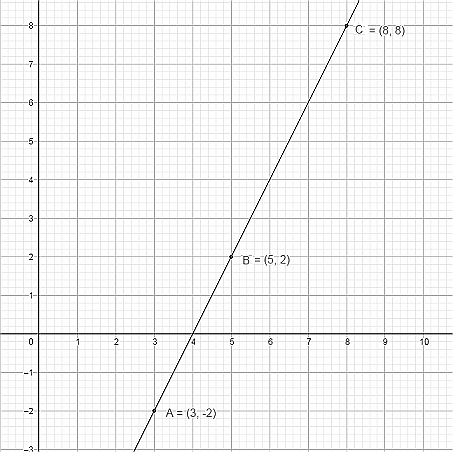
Let's say that the points are A(x1,y1)=(3,−2)A\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,-2 \right) , B(x2,y2)=(5,2)B\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,2 \right) and C(x3,y3)=(8,8)C\left( {{x}_{3}},{{y}_{3}} \right)=\left( 8,8 \right) .
We know that, using the section formula, that for the points to be collinear: mn=x1−x3x3−x2=y1−y3y3−y2\dfrac{m}{n}=\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}} .
Here, x1−x3x3−x2=3−88−5=−53\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{3-8}{8-5}=\dfrac{-5}{3} and y1−y3y3−y2=−2−88−2=−106=−53\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}}=\dfrac{-2-8}{8-2}=\dfrac{-10}{6}=\dfrac{-5}{3}.
Since both the values are the same, the points are collinear. Also, a negative value of mn=−53\dfrac{m}{n}=\dfrac{-5}{3} suggests that the point C is outside AB and the ratio AC : BC = 5 : 3.
The position of the three points is shown below:

Note:

  1. There are many ways to show that three points A, B and C are collinear (in a straight line):
  2. Section formula (Ratio / Slope method).
  3. Distance method: AB + BC = AC.
  4. Area method: Area of Δ ABC = 0.