Question
Question: Should $\int_{1}^{2}x^2-5x+6 = \int_{3}^{4}x^2-5x+6 ?$ [Because it is an even and symmetrical func...
Should
∫12x2−5x+6=∫34x2−5x+6?
[Because it is an even and symmetrical function?]
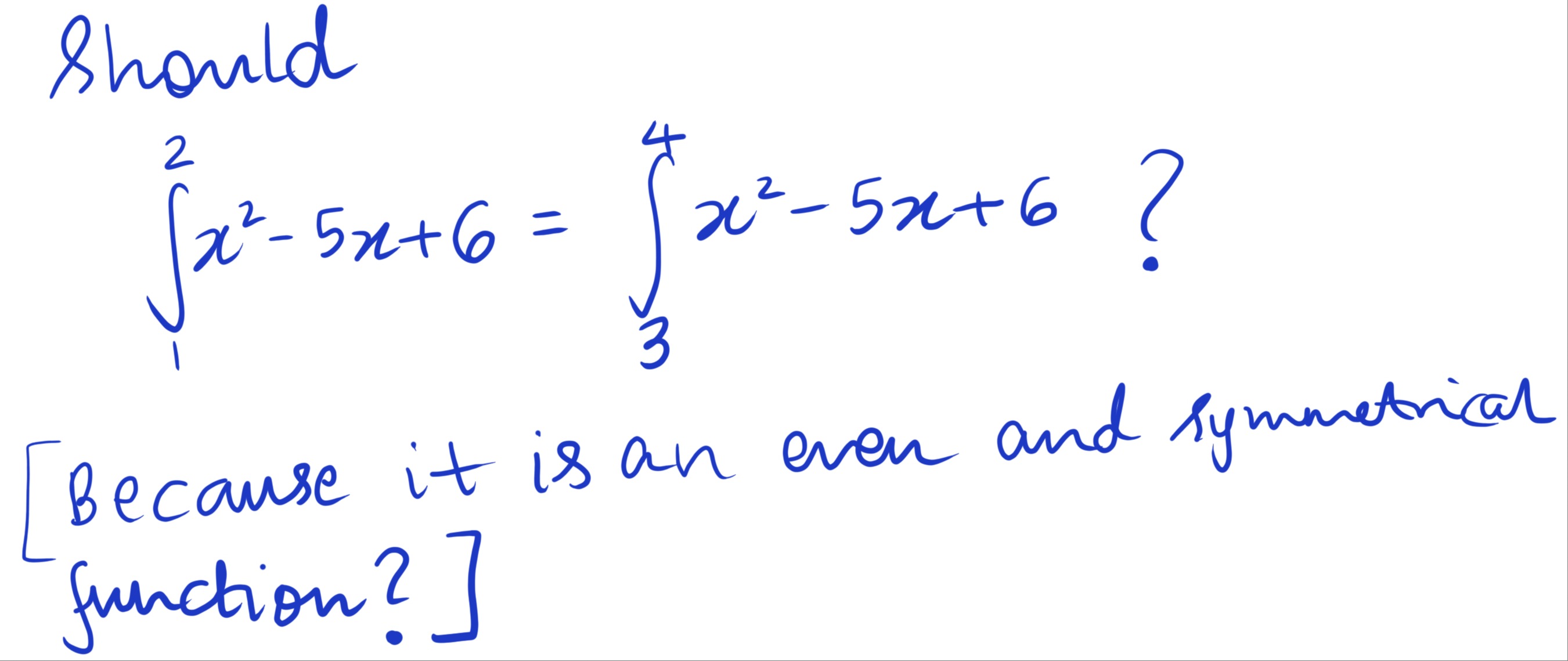
Yes
No
Yes
Solution
The given question asks whether the definite integral of the function f(x)=x2−5x+6 from 1 to 2 is equal to its definite integral from 3 to 4, based on the premise that it is an even and symmetrical function.
1. Analyze the function for symmetry: The function f(x)=x2−5x+6 is a quadratic function, which represents a parabola. The axis of symmetry for a parabola ax2+bx+c is given by x=−2ab. For f(x)=x2−5x+6, we have a=1 and b=−5. So, the axis of symmetry is x=−2×1(−5)=25=2.5. A function f(x) is symmetric about the line x=a if f(a−h)=f(a+h) for any real number h. Let's check this for a=2.5: f(2.5−h)=(2.5−h)2−5(2.5−h)+6=(6.25−5h+h2)−(12.5−5h)+6=6.25−5h+h2−12.5+5h+6=h2−0.25. f(2.5+h)=(2.5+h)2−5(2.5+h)+6=(6.25+5h+h2)−(12.5+5h)+6=6.25+5h+h2−12.5−5h+6=h2−0.25. Since f(2.5−h)=f(2.5+h), the function f(x) is indeed symmetric about the line x=2.5. Note: The term "even function" specifically refers to symmetry about the y-axis (x=0). While f(x) is symmetric, it is not an "even function" in the standard definition.
2. Analyze the integration intervals for symmetry: The first interval is [1,2]. The second interval is [3,4]. Let's express these intervals relative to the axis of symmetry x=2.5. For [1,2]: 1=2.5−1.5 2=2.5−0.5 So, the interval is [2.5−1.5,2.5−0.5].
For [3,4]: 3=2.5+0.5 4=2.5+1.5 So, the interval is [2.5+0.5,2.5+1.5].
We can see that if we have an axis of symmetry at x=a, and two intervals are [a−k2,a−k1] and [a+k1,a+k2], then these intervals are symmetrically placed with respect to x=a.
3. Property of definite integrals for symmetric functions and intervals: If a function f(x) is symmetric about x=a (i.e., f(a−h)=f(a+h)), then for any real numbers k1 and k2: ∫a−k2a−k1f(x)dx=∫a+k1a+k2f(x)dx This property holds because the graph of the function over the interval [a−k2,a−k1] is a mirror image of the graph over [a+k1,a+k2] with respect to the line x=a. Consequently, the signed areas under the curve for these symmetric intervals will be equal.
4. Conclusion: Since the function f(x)=x2−5x+6 is symmetric about x=2.5, and the intervals [1,2] and [3,4] are symmetrically placed with respect to x=2.5 (as [2.5−1.5,2.5−0.5] and [2.5+0.5,2.5+1.5] respectively), the definite integrals over these intervals must be equal.
Verification by direct calculation: First, find the indefinite integral: ∫(x2−5x+6)dx=3x3−25x2+6x+C Let F(x)=3x3−25x2+6x.
For the first integral: ∫12(x2−5x+6)dx=F(2)−F(1) F(2)=323−25(22)+6(2)=38−220+12=38−10+12=38+2=38+6=314 F(1)=313−25(12)+6(1)=31−25+6=62−15+36=623 ∫12(x2−5x+6)dx=314−623=628−23=65
For the second integral: ∫34(x2−5x+6)dx=F(4)−F(3) F(4)=343−25(42)+6(4)=364−25(16)+24=364−40+24=364−16=364−48=316 F(3)=333−25(32)+6(3)=327−25(9)+18=9−245+18=27−245=254−45=29 ∫34(x2−5x+6)dx=316−29=632−27=65 Both integrals are equal to 65.
Therefore, the statement is true.
The reason provided in the question is partially correct but could be more precise. The function is symmetric about x=2.5, and the integration intervals are symmetric with respect to this axis.
