Solveeit Logo
Login

Question

Question: Ship A is sailing towards the north east with velocity \(\vec v = 30\hat i + 50\hat jkm/hr\) where \...

Ship A is sailing towards the north east with velocity v⃗=30i^+50j^km/hr\vec v = 30\hat i + 50\hat jkm/hr where i^\hat i points east j^\hat j and north. Ship B is at a distance of 80 km east and 150 km north of ship A and is sailing towards west at 10 km/hr. A will be at minimum distance from B in
(A) 4.24.2 hours
(B) 2.22.2 hours
(C) 3.23.2 hours
(D) 2.62.6 hours

Explanation

Solution

We know that the relation between time, velocity and displacement is given as
Time =displacementvelocity = \dfrac{{displacement}}{{velocity}}
And the above expression is also applicable for relative motion like relative velocity, relative displacement etc. But time does not depend on frame of reference.

Complete step by step answer:

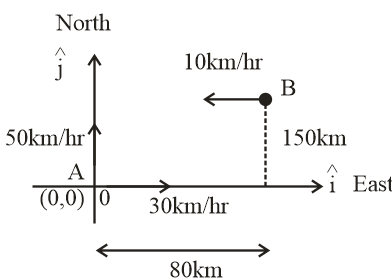
Given that initial positions of ship A & B is
r⃗A=0i^+0j^{\vec r_A} = 0\hat i + 0\hat j …..(1)
r⃗B=(80i^+150j^)km{\vec r_B} = (80\hat i + 150\hat j)km ….(2)
So, the relative position of B with respect to A
r⃗BA=(80i^+150j^)km{\vec r_{BA}} = (80\hat i + 150\hat j)km …..(3)
Also, given that the velocity of ship A & B is
v⃗A=(30i^+50j^)km/hr{\vec v_A} = (30\hat i + 50\hat j)km/hr
v⃗B=−10i^km/hr{\vec v_B} = - 10\hat ikm/hr
So, relative velocity of B with respect to A is
v⃗BA=−10i^−(30i^+50j^){\vec v_{BA}} = - 10\hat i - (30\hat i + 50\hat j)
=−10i^−30i^−50j^= - 10\hat i - 30\hat i - 50\hat j
v⃗BA=−40i^−60j^{\vec v_{BA}} = - 40\hat i - 60\hat j …..(4)
And magnitude of v⃗AB{\vec v_{AB}} is given as
∣v⃗BA∣=(40)2+(50)2|{\vec v_{BA}}| = \sqrt {{{(40)}^2} + {{(50)}^2}}
1600+2500\sqrt {1600 + 2500}
∣v⃗BA∣=4100|{\vec v_{BA}}| = \sqrt {4100} …..(5)
We know that
Time t =displacement(r⃗)velocity(v⃗) = \dfrac{{displacement(\vec r)}}{{velocity(\vec v)}}
In relative motion
t=r⃗BAv⃗BAt = \dfrac{{{{\vec r}_{BA}}}}{{{{\vec v}_{BA}}}}
On multiplying v⃗BA⇒t=r⃗BA⋅v⃗BAv⃗BA⋅v⃗BA{\vec v_{BA}} \Rightarrow t = \dfrac{{{{\vec r}_{BA}} \cdot {{\vec v}_{BA}}}}{{{{\vec v}_{BA}} \cdot {{\vec v}_{BA}}}}
t=r⃗BA⋅v⃗BA∣v⃗BA∣2t = \dfrac{{{{\vec r}_{BA}} \cdot {{\vec v}_{BA}}}}{{|{{\vec v}_{BA}}{|^2}}}
So, from equation 3, 4 & 5
t=(80i^+150j^)⋅(−40i^−50j^)(4100)2t = \dfrac{{(80\hat i + 150\hat j) \cdot ( - 40\hat i - 50\hat j)}}{{{{(\sqrt {4100} )}^2}}}
t=[−(80×40)]+[−(150×50)]4100t = \dfrac{{[ - (80 \times 40)] + [ - (150 \times 50)]}}{{4100}}
t=−3200−75004100=−107004100t = \dfrac{{ - 3200 - 7500}}{{4100}} = \dfrac{{ - 10700}}{{4100}}
Time never be –ve, hence
t=107004100=10741=2.6t = \dfrac{{10700}}{{4100}} = \dfrac{{107}}{{41}} = 2.6 hours
t=2.6t = 2.6 hours

So, the correct answer is “Option D”.

Note:
Relative motion is a concept which makes numerical problems easy. We can apply the above formulae only when there is no acceleration given to particles. Time does not depend on frame of reference.