Question
Question: Shankar made the following picture also. What shapes can they be broken into so that we can find t...
Shankar made the following picture also.
What shapes can they be broken into so that we can find the area easily?
Make some more pictures and think of the shapes they can be divided into different parts.
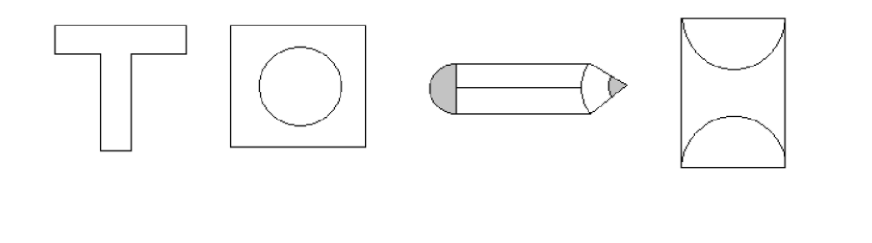
Solution
We know the formula to find the areas of a rectangle/square, parallelogram, triangle, and circle.
Breaking a complicated shape into the shapes whose formulae we already know, can help us determine its area.
Look for the familiar shapes, like rectangle or a circle, in the given pictures.
Complete step by step solution:
The given shapes can be divided into rectangles, circles, semi-circles and triangles as illustrated below.
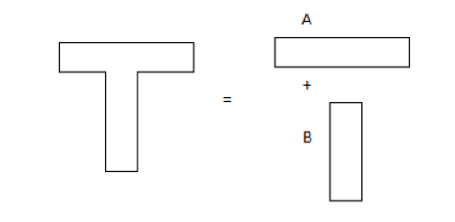
The T shape can be divided into two rectangles, as shown:
Total area = A+B .
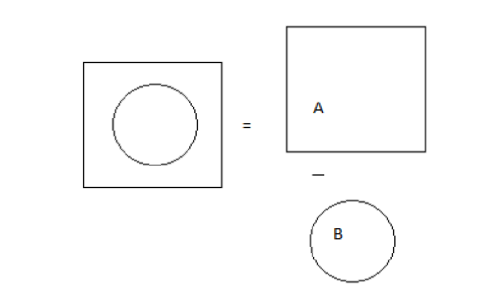
We can separate the square and the circle in the next shape.
Total area = A−B .
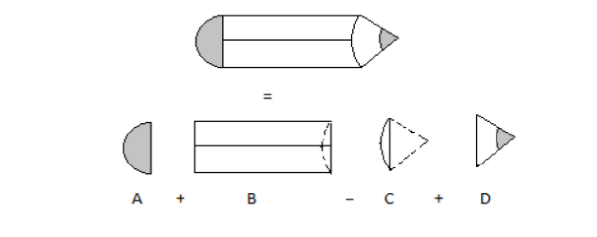
For the pencil, we can divide into a semi-circle, a rectangle, a segment of a circle and a triangle.
Total area = A+B−C+D .
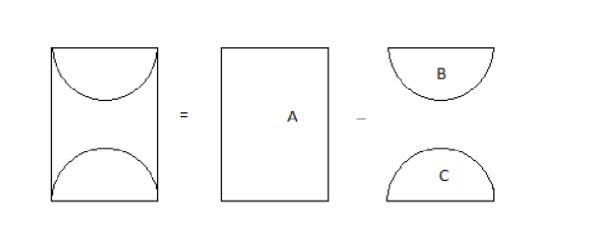
The next shape is made up of a rectangle and two semi-circles.
Total area = A−B−C .
Note: Area is measured by counting the number of squares of a unit length present in a shape.There are a×a unit squares inside a square of side a units.
Area of a parallelogram with base b units and height h units is b×h square units.
Area of a triangle with base b units and height h units will be 21×b×h square units.
Area of a circle of radius r units, is πr2 sq. units.
3D figures are also made by combining basic figures such that squares, rectangles, circles etc. For example: Cube is a 3D figure containing six squares having area 2a if a is the length of the side of the square and thus, Total area of the cube is 26a as it contains six squares.
