Question
Question: Seven resistance are connected between points A and B as shown in the adjoining figure. The equivale...
Seven resistance are connected between points A and B as shown in the adjoining figure. The equivalent resistance between A and B is
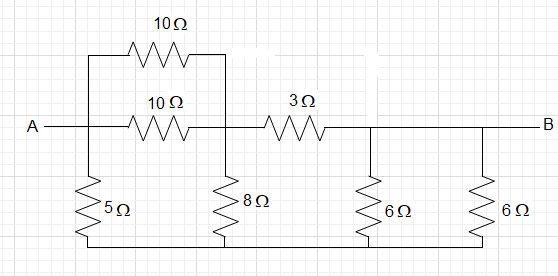
A. 5Ω
B. 4.5Ω
C. 4Ω
D. 3Ω
Solution
Hint: Use the formula for the equivalent resistance of resistance in series connection and parallel connection. First, simplify the resistances that are in parallel and proceed further. Check the ratio of resistances for a balanced wheatstone bridge.
Formula used:
Req1=R11+R21+R31+.......+Rn1
Req=R1+R2+R3+R4+.......+R5
Complete step by step answer:
Whenever we have a question of calculating the effective or equivalent resistance of the given connection of several resistances, work on the resistances that are in parallel connection.
If two or more have both the ends in common or same potential difference then the resistances are said to be in parallel connection. Suppose n resistances are in parallel connection. Then the reciprocal of the equivalent resistance of this connection is equal to the sum of the reciprocal of each of the individual resistances.
i.e. Req1=R11+R21+R31+.......+Rn1.
When n resistances are series connection (same current passes through all), the equivalent resistances is equal to the sum of the individual resistances.
i.e. Req=R1+R2+R3+R4+.......+R5
Now, let us see which resistances are in parallel connection.
The two resistances of 10Ω are in parallel.
The reciprocal of equivalent resistance of these two will be:
Req1=101+101=102=51
Now, we can remove both the resistances and replace the set by a resistance of 5Ω.
⇒Req=5Ω.
The resistances of 6Ω are also in parallel connection.
Therefore,
Req1=61+61=62=31
⇒Req=3Ω
Now, we can remove both the resistances and replace the set by a resistance of 3Ω.
Now the connection will look like:
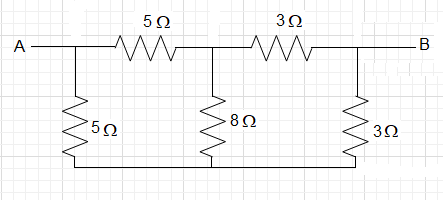
If we observe the connection properly, it looks like a wheatstone bridge connection. And for our good luck the bridge is balanced because the equation R2R1=R4R3 is satisfied.
Therefore, no current will flow through the resistance of 8Ω.
Hence, it can be removed from the connection.
Now the connection will look like:
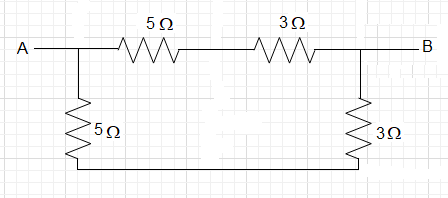
As we can see that the resistances of 5Ω and 3Ω are in series connection.
Therefore, Req=5+3=8Ω
Hence, the connection will simplify to:
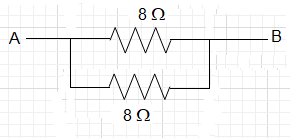
Now the resistances are in parallel.
Hence, Req1=81+81=82=41
⇒Req=4Ω.
Therefore, the equivalent resistance of the whole connection across A and B is 4Ω.
Hence, the correct option is C.
Note: When R2R1=R4R3 is satisfies, this means that the potential difference across the resistance of 8Ω is zero. So we can also remove this resistance and join the ends points of the resistance. In other words, short this resistance.
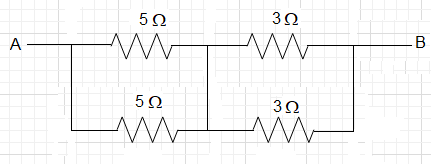
Now, we can see that the two pairs of resistance are in parallel.
Therefore,
Req11=51+51=52⇒Req1=25Ω
Req21=31+31=32⇒Req2=23Ω
Therefore, the equivalent resistance of the circuit is,
Req=25+23=28=4Ω.
Hence, we can find the equivalent resistance of a balanced wheat stone bridge in two ways.
