Question
Question: . Seven identical discs are arranged in a hexagonal planar pattern so as to touch each neighbor, as ...
. Seven identical discs are arranged in a hexagonal planar pattern so as to touch each neighbor, as shown in the figure. Each disc has mass m and radius r. What is the moment of inertia of the system of seven discs about an axis passing through the center of the central disc and normal to the plane of all discs.
(A) 27mr2
(B) 213mr2
(C) 229mr2
(D) 255mr2
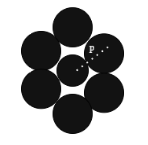
Solution
Hint It is given that all 7 remain in contact. Use the parallel axis theorem for moment of inertia of 6 discs and find the moment of inertia of the central disc. Again, use the parallel axis theorem to find the total inertia about point O.
Complete Step By Step Solution:
First it is required to find the moment of inertia of the center ,
We know that moment of inertia of a disc object is 2mr2,
Now using the parallel axis theorem , which implies that moment of inertia about point O is the algebraic sum of Moment of inertia of center mass and the product of mass and distance squared.
Mathematically,
Io=Icm+Md2
Here, Icmis the moment of inertia of the center disc.
Now, here M= 6*M since there are 6 discs surrounding the central disc. Hence the Moment of inertia about the center of mass will be the moment of inertia about center disc plus moment of inertia about 6 discs.
Now,
Io=Icm+Md2
Substituting the values for M and Icm, we get,
Io=27mr2+Md2
We know that distance between the center point of the central disc to the center point of the surrounding discs as d=2r, Applying this in the equation above and changing M as m, we get
Io=27mr2+6m(2r)2
Simplifying and solving the terms,
Io=27mr2+24m(r)2
Taking LCM we get the final equation as
Io=255mr2
Hence, option (d) is the right answer.
Note:
Parallel axis theorem states that moment of inertia about a parallel axis passing through the center of mass is the algebraic sum of moment of inertia of the body about an axis passing through the center of mass and product of mass and square distance between the objects.
