Question

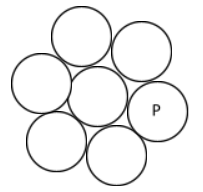
Seven identical coins are rigidly arranged on a flat table in the pattern shown below so that each coin touches its neighbours. Each coin is a thin disc of mass m and radius r. Note that the moment of inertia of an individual coin about an axis passing through the centre and perpendicular to the plane of the coin is $\dfrac{{m{r^2}}}{2}$.
The moment of inertia of the system of seven coins about an axis that passes through the point P (the centre of the coin positioned directly to the right of the central coin) and perpendicular to the plane of the coins is

Answer 1

Use Parallel Axis theorem as it states that, the moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of inertia of body about axis passing through the center and product of mass of the body times the square of distance between two axes and to find moment of Inertia the formula is given as
$I = {I_c} + M{h^2}$

Complete step by step answer:
To find the Moment of Inertia of the system of seven coins about an axis that passes through the point P and perpendicular to the plane of the coins, apply Parallel Axis theorem.
Hence, Parallel Axis theorem is represented as
$I = {I_c} + M{h^2}$
As mentioned in the question that moment of Inertia of an individual coin about an axis passing through centre and perpendicular to the plane of the coin is $\dfrac{{m{r^2}}}{2}$. Applying this we get
${I_{cm}} = \left( {\dfrac{{m{r^2}}}{2} + 4m{r^2}} \right) \times 6 + \dfrac{{m{r^2}}}{2}$
After simplification we get
${I_{cm}} = \dfrac{{55m{r^2}}}{2}$
Using Parallel axis theorem
${I_p} = \dfrac{{55m{r^2}}}{2} + 28m{r^2}$
Hence, we get
${I_p} = \dfrac{{111m{r^2}}}{2}$
Therefore, the moment of inertia of the system of seven coins about an axis that passes through the point P (the centre of the coin positioned directly to the right of the central coin) and perpendicular to the plane of the coins is $\dfrac{{111m{r^2}}}{2}$.
Formula used:
$I = {I_c} + M{h^2}$
In which,
$I$= moment of inertia of body
${I_c}$= moment of inertia about center
$M$= mass of the body
${h^2}$= is distance between two axes

Note:
To find moment of Inertia of the any system, just apply the formula of inertia, which states that, the moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of inertia of body about the axis passing through the center and product of mass of the body times the square of distance between the two axes.