Question
Question: Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown...
Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is?
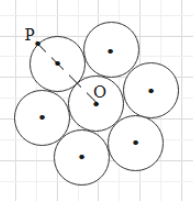
Solution
To solve this we must have the knowledge of the parallel axes theorem that is used to find the moment of inertia about an axis with the help of the moment of inertia about the centre of mass. Use the theorem when needed and calculate the moment of inertia about the given axis.
Formula used:
Icom+Md2=Ip
Complete step by step answer:
To find the moment of inertia of the given arrangement we will write the moment of inertia of each disk about an axis passing through their centres and perpendicular to their planes.
The moment of inertia of a planar disk about an axis passing through its centre and perpendicular to its plane is equal to I=2MR2,
where M is the mass and R is the radius of the disk.
Now, we will calculate the moment of inertia of each disk about an axis passing through point O and perpendicular to the plane of the disks. For this, we will use the parallel axes theorem. According to this theorem, Icom+Md2=Ip …..(i).
Here, Icom is the moment of inertia of a planar body about an axis passing through its centre of mass, Ip is the moment of inertia of the body about an axis passing through point P and parallel to the axis passing through the centre of mass and d is the perpendicular distance between the two axes.
We have to find the moment of inertia of the outer 6 disks about an axis passing through point O and perpendicular to the plane. The centre of mass of a circular disk is located at the centre of the disk.
⇒Icom=I=2MR2 (For each disk)
In this case, d=2R and Ip=Io.
Substitute the values in (i)
⇒2MR2+M(2R)2=IO
⇒IO=29MR2.
This means that the moment of inertia of each of the 6 disks is equal to 29MR2.
Therefore, the moment of inertia of the whole arrangement about a perpendicular axis passing through point O is 6(29MR2)+2MR2=255MR2.
It is easy to understand that point O is the location of the centre of mass of the whole arrangement. (Due to symmetry).
Now, use the parallel axes theorem once again to obtain the moment of inertia of the system about a perpendicular axis passing through point P.
In this case, Icom=255MR2 and d=3R.
And note that the mass of the system will be 7M.
Substitute these values in (i).
Ip=255MR2+7M(3R)2 ⇒Ip=(255+126)MR2 ∴Ip=2181MR2.
Therefore, the moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is equal to 2181MR2.
Note: Note that we could perform all the operations because moment of inertia is a scalar quantity. Therefore, we can add it algebraically. Also, note that the parallel axes theorem is only applicable from planar bodies. It does not work with three dimensional bodies.
