Question

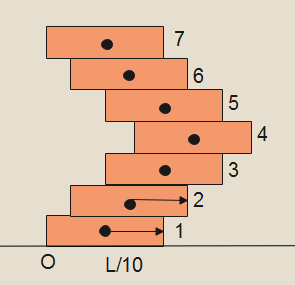
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x coordinate of the center of mass relative to the origin O.

Answer 1

In this question, we will use the basic formula for the center of mass system. This will help us to get the required result. Also, we will study the basics of the term mass and we will also see some basic concepts of the center of mass system, for our better understanding.

Formula used:
$X = \sum\limits_{i = 0}^n {\dfrac{{{m_i}{x_i}}}{M}}$

Complete answer:
Here, we have seven homogeneous bricks, each of length L. now, we will see x coordinate of each brick one by one.
x- Coordinate of center of mass of brick 1 is $\dfrac{L}{2}$
x- Coordinate of center of mass of brick 2 is$\dfrac{L}{2} + \dfrac{L}{{10}}$
x- Coordinate of center of mass of brick 3 is$\dfrac{L}{2} + \dfrac{L}{{10}} + \dfrac{L}{{10}}$
x- Coordinate of center of mass of brick 4 is$\dfrac{L}{2} + \dfrac{L}{{10}} + \dfrac{L}{{10}} + \dfrac{L}{{10}}$
x- Coordinate of center of mass of brick 5 is$\dfrac{L}{2} + \dfrac{L}{{10}} + \dfrac{L}{{10}}$
x- Coordinate of center of mass of brick 6 is$\dfrac{L}{2} + \dfrac{L}{{10}}$
x- Coordinate of center of mass of brick 7 is$\dfrac{L}{2}$
So, from above observations we can find the x-coordinate of the combined system as:
$X = \sum\limits_{i = 0}^n {\dfrac{{{m_i}{x_i}}}{M}}$
$X = \dfrac{{\left( {m.\dfrac{L}{2}} \right) + \left( {m.\dfrac{{6L}}{{10}}} \right) + \left( {m.\dfrac{{7L}}{{10}}} \right) + \left( {m.\dfrac{{8L}}{{10}}} \right) + \left( {m.\dfrac{{7L}}{{10}}} \right) + \left( {m.\dfrac{{6L}}{{10}}} \right) + \left( {m.\dfrac{L}{2}} \right)}}{{m + m + m + m + m + m + m}}$
\eqalign{& \Rightarrow X = \dfrac{{44L}}{{7 \times 10}} \cr & \therefore X = \dfrac{{22L}}{{35}} \cr}
Therefore, we get the required answer for the x-coordinate of the center of mass for the given system.

Additional information:
As we know that, the term mass is defined as the property of a physical body and also the measure of its resistance to acceleration, when a net force is applied on that body or object. Now, the mass of any object or body also tells us the strength of its gravitational attraction to other bodies. Also, we know that the basic S.I unit of mass is the kilogram represented by kg.
Let us know something about the center of mass; it is a position which is defined as relative to an object or system of objects. Center of mass is the average position of all the given parts of the system or body, weighted according to their given masses. Now, for a simple rigid object having uniform density, the center of mass is located or can be observed at the centroid.
The center of mass is the distribution of mass in space, which is a unique point. On this point the weighted relative position of the distributed mass of the object or the system sums to zero.

Note:
We should remember that the concept of centre of mass i.e., COM can be used to analyze the complicated motion of the system or the given object, generally when two and more objects collide or when an object explodes into its constituent fragments.