Question
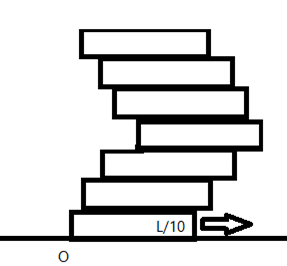
Question: Seven homogeneous bricks each of length \(L\) are arranged as shown in figure. Each brick is displac...
Seven homogeneous bricks each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by 10L, then the x-coordinate of centre of mass relative to the origin shown.
Solution
We know that the centre of mass is the point of the system where the whole mass of the system is concentrated. When some external force is applied over this point the body experiences linear acceleration without any angular acceleration.
Formula used:
xcm=m1+m2+m3m1x1+m2x2+m3x3
Complete answer:
Centre of mass is written as COM in short. It is a point where the given objects can be balanced, hence is also called the balancing point. We know that for a point mass body, the mass is concentrated at that point. However, for bodies which are not point sized or macroscopic in nature, the mass of the body is distributed all over the given body. Also at the COM, the sum of the distribution of mass is zero. Thus, for easy calculation, the COM is taken.
Here, we are given 7 sticks of the same nature as shown in the figure; let us assume that the mass of the sticks are m
Let us assume that the sticks are rigid. Then, the COM of the lowest stick lies in the geometrical centre of the stick.
Then the COM of the of the lowest stick is given as x1=m(2L)
If that the stick is displaced by 10L, then the COM of the stick is given as x2=m(2L+10L)=106mL
Similarly, COM of the 3rd stick from the lowest is given as x3=m(2L+10L+10L)=107mL
Similarly, COM of the 4th stick from the lowest is given as x4=m(2L+10L+10L+10L)=108mL
Similarly, COM of the 5th stick from the lowest is given as, here since the body is towards the left, we get, x5=m(2L+10L+10L+10L−10L)=107mL
Similarly, COM of the 6th stick from the lowest is given as, here since the body is towards the left, we get, x6=m(2L+10L+10L+10L−10L−10L)=106mL
Similarly, the Similarly, COM of the 7th stick from the lowest is given as, here since the body is towards the left, we get, x7=m(2L+10L+10L+10L−10L−10L−10L)=2mL
Then the COM of the system is given as xcm=7m2mL+106mL+107mL+108mL+107mL+106mL+2mL
xcm=7m22mL+1012mL+1014mL+108mL
xcm=70m10mL+12mL+14mL+8mL
xcm=70m44mL
xcm=7044L=3522L
Note:
In rigid bodies, the COM is generally the centroid or the geometric centre of the given body and it lies inside the body. However for irregular bodies and hollow bodies, the COM lies outside the given body. The COM is used generally as a point of reference.
