Question
Question: Let $a_1, a_2, a_3,...$ be a G.P. such that $a_1 < 0, a_1 + a_2 = 4$ and $a_3 + a_4 = 16$. If $\sum_...
Let a1,a2,a3,... be a G.P. such that a1<0,a1+a2=4 and a3+a4=16. If ∑i=19ai=4λ, then λ is equal to:
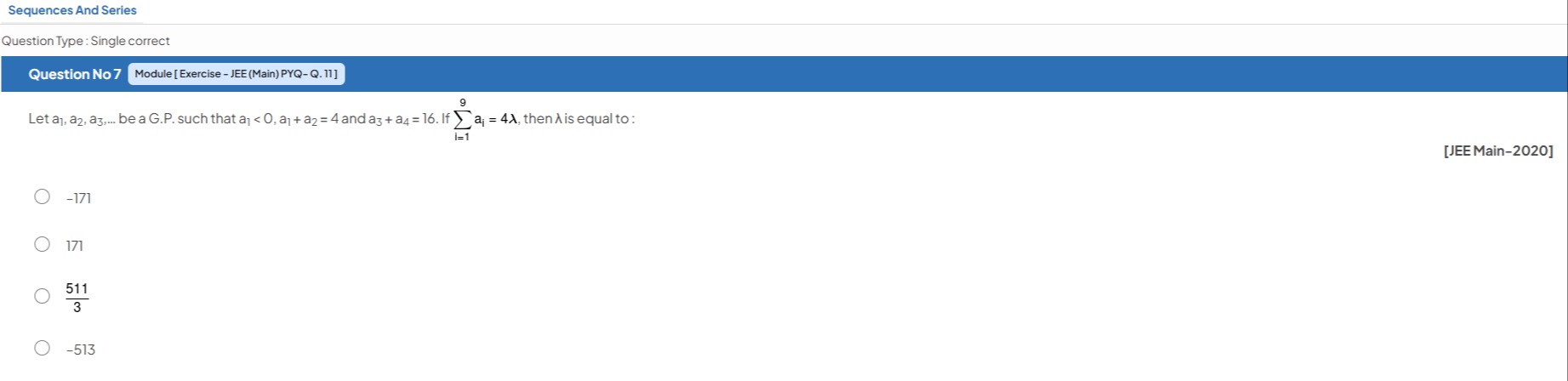
-171
171
3511
-513
-171
Solution
The problem provides information about a Geometric Progression (G.P.) and asks us to find the value of λ based on the sum of its first nine terms.
Let the first term of the G.P. be a and the common ratio be r. The n-th term of a G.P. is given by an=arn−1.
We are given the following conditions:
- a1<0⟹a<0.
- a1+a2=4. Substituting the terms in terms of a and r: a+ar=4 a(1+r)=4 (Equation 1)
- a3+a4=16. Substituting the terms in terms of a and r: ar2+ar3=16 ar2(1+r)=16 (Equation 2)
Now, we can solve these two equations to find the values of a and r. Divide Equation 2 by Equation 1: a(1+r)ar2(1+r)=416 r2=4 This gives two possible values for r: r=2 or r=−2.
Case 1: r=2 Substitute r=2 into Equation 1: a(1+2)=4 3a=4 a=34 However, this value of a contradicts the given condition a1<0 (i.e., a<0). Therefore, r=2 is not the correct common ratio.
Case 2: r=−2 Substitute r=−2 into Equation 1: a(1+(−2))=4 a(1−2)=4 a(−1)=4 a=−4 This value of a satisfies the condition a1<0. Thus, the first term is a=−4 and the common ratio is r=−2.
Next, we need to find the sum of the first nine terms of this G.P., denoted as ∑i=19ai=S9. The sum of the first n terms of a G.P. is given by the formula Sn=1−ra(1−rn), provided r=1. Here, a=−4, r=−2, and n=9.
S9=1−(−2)−4(1−(−2)9) Calculate (−2)9: (−2)9=−(29)=−512
Substitute this value back into the sum formula: S9=1+2−4(1−(−512)) S9=3−4(1+512) S9=3−4(513)
Now, simplify the expression: 513÷3=171 S9=−4×171 S9=−684
The problem states that ∑i=19ai=4λ. So, we have: −684=4λ
To find λ, divide both sides by 4: λ=4−684 λ=−171
