Question
Question: If G be the GM between x and y, then the value of $\frac{1}{G^2-x^2}+\frac{1}{G^2-y^2}$ is equal to...
If G be the GM between x and y, then the value of G2−x21+G2−y21 is equal to
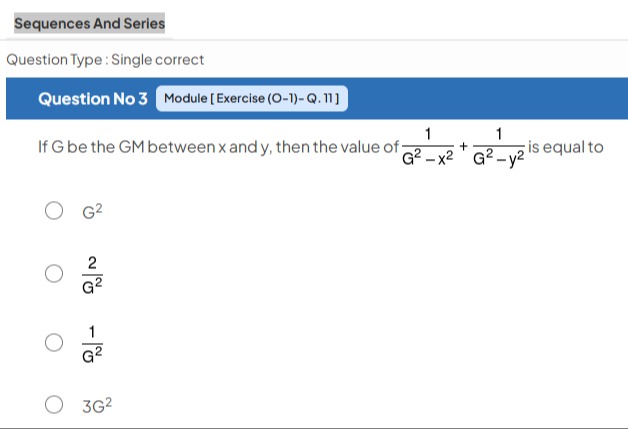
G2
G22
G21
3G2
G21
Solution
1. Understanding the Geometric Mean (GM):
If G is the Geometric Mean (GM) between two numbers x and y, then by definition: G2=xy
2. Substituting into the Expression:
The given expression is G2−x21+G2−y21. Substitute G2=xy into the expression:
xy−x21+xy−y21
3. Factoring the Denominators:
Factor out common terms from each denominator:
- xy−x2=x(y−x)
- xy−y2=y(x−y)
So the expression becomes:
x(y−x)1+y(x−y)1
4. Adjusting for Common Denominators:
Notice that (x−y) is the negative of (y−x), i.e., (x−y)=−(y−x). Substitute this into the second term:
x(y−x)1+y(−(y−x))1
x(y−x)1−y(y−x)1
5. Combining the Fractions:
Now, find a common denominator, which is xy(y−x):
xy(y−x)y−xy(y−x)x
Combine the numerators:
xy(y−x)y−x
6. Simplifying the Expression:
Assuming x=y (otherwise the original expression would be undefined due to division by zero), we can cancel out the term (y−x) from the numerator and the denominator:
xy1
7. Final Substitution:
Recall from step 1 that G2=xy. Substitute this back into the simplified expression:
G21
Thus, the value of the expression is G21.
