Question

In a GP, first term is 1. If $4T_2 + 5T_3$ is minimum, then its common ratio is

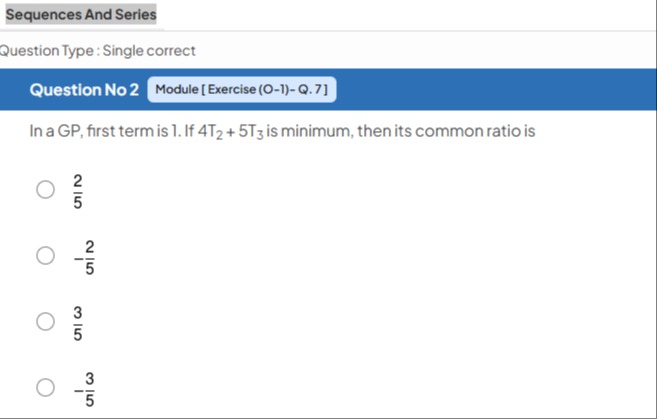
• A. $\frac{2}{5}$
• B. $-\frac{2}{5}$
• C. $\frac{3}{5}$
• D. $-\frac{3}{5}$

Answer 1

Answer: (B)

$-\frac{2}{5}$

Answer 2

To find the common ratio ($r$) of a Geometric Progression (GP) when the first term is 1 and the expression $4T_2 + 5T_3$ is minimum:

1. Express $T_2$ and $T_3$ in terms of the first term $a=1$ and common ratio $r$. This gives $T_2 = r$ and $T_3 = r^2$.
2. Formulate the expression to be minimized: $E(r) = 4T_2 + 5T_3 = 4r + 5r^2$.
3. Recognize that $E(r)$ is a quadratic function of $r$. Since the coefficient of $r^2$ is positive (5), the parabola opens upwards, indicating a minimum value.
4. Find the value of $r$ at which this minimum occurs. This can be done by setting the first derivative of $E(r)$ with respect to $r$ to zero, or by using the vertex formula for a parabola ($r = -B/(2A)$).
5. Differentiating $E(r)$ gives $10r + 4$. Setting this to zero yields $10r = -4$, so $r = -4/10 = -2/5$.
6. The second derivative is $10$, which is positive, confirming it's a minimum.

Therefore, the common ratio is $-\frac{2}{5}$.