Question

Select the correct statement from $\left( 1 \right),\left( 2 \right),\left( 3 \right)and\left( 4 \right).$ The function $f\left( x \right) = x{e^{1 - x}}$ ;
$\left( 1 \right)$ Strictly increases in the interval $\left( {\dfrac{1}{2},2} \right)$
$\left( 2 \right)$ Increases in the interval $\left( {0,\infty } \right)$
$\left( 3 \right)$ Decreases in the interval $\left( {0,2} \right)$
$\left( 4 \right)$ Strictly decreases in the interval $\left( {1,\infty } \right)$

Answer 1

To solve this type of questions, there is a sequence of steps which needs to be followed.
$\left( 1 \right)$ Calculate $f'\left( x \right)$ that is the first derivative of the given function with respect to $x$.
$\left( 2 \right)$ Put $f'\left( x \right) = 0$ to find the critical values.
$\left( 3 \right)$ If we get multiple values then arrange them in ascending order, for example if we get $x = 2,3$ .
$\left( 4 \right)$ Define the intervals like this ; the first one would be always from $- \infty$ to first critical point , example: $\left( { - \infty ,2} \right)$ , second interval will be from first critical point to another like here $\left( {2,3} \right)$ and the last one will be from last critical point to $\infty$ , example: $\left( {3,\infty } \right)$.
$\left( 5 \right)$ Check the sign of $f'\left( x \right)$ for each interval to analyze the behavior of the derivative .

Complete step-by-step solution:
We know that, $\left( 1 \right){\text{ }}f\left( x \right)$ is strictly increasing when $f'\left( x \right) > 0$ ( positive ) and $\left( 2 \right){\text{ }}f\left( x \right)$ is strictly decreasing when $f'\left( x \right) < 0$ ( negative ) . So, first we need to differentiate the given function; $f\left( x \right) = x{e^{1 - x}}$ .
$\Rightarrow f\left( x \right) = x{e^1}{e^{ - x}}$
Simplifying the above function, to convert it into fractional form so that it can be easily differentiated;
$\Rightarrow f\left( x \right) = \dfrac{{xe}}{{{e^x}}}$
The above function can be solved by the division rule of differentiation;
\left( {\because \dfrac{d}{{dx}}\left\\{ {\dfrac{u}{v}} \right\\} = \dfrac{{\dfrac{{du}}{{dx}} \times v - u \times \dfrac{{dv}}{{dx}}}}{{{v^2}}}} \right)
Let $u = xe{\text{ and }}v = {e^x}{\text{ }}$;
$\therefore f'\left( x \right) = \dfrac{{\left( e \right) \times {e^x} - \left( {xe} \right)\left( {{e^x}} \right)}}{{{{\left( {{e^x}} \right)}^2}}}$
Taking ${e^x}$ outside in the numerator;
$\Rightarrow f'\left( x \right) = \dfrac{{{e^x}\left( {e - xe} \right)}}{{{e^{2x}}}}$
On further simplification;
$\Rightarrow f'\left( x \right) = \dfrac{{e\left( {1 - x} \right)}}{{{e^x}}}$
Since $e$ is Euler’s number ( also the base of natural logarithm ) and it has a constant value approximately equal to $2.71828$ , therefore the factor $\dfrac{e}{{{e^x}}}$ is always positive or $\dfrac{e}{{{e^x}}} > 0$ .
So, to analyze the behavior of the function we have to only check the factor $\left( {1 - x} \right)$ .
Put $\left( {1 - x} \right) = 0$ to find the critical point;
$\Rightarrow - x + 1 = 0$
$\Rightarrow x = 1$
Let us consider two intervals , when $x \in \left( { - \infty ,1} \right){\text{ and x}} \in \left( {1,\infty } \right)$ ;

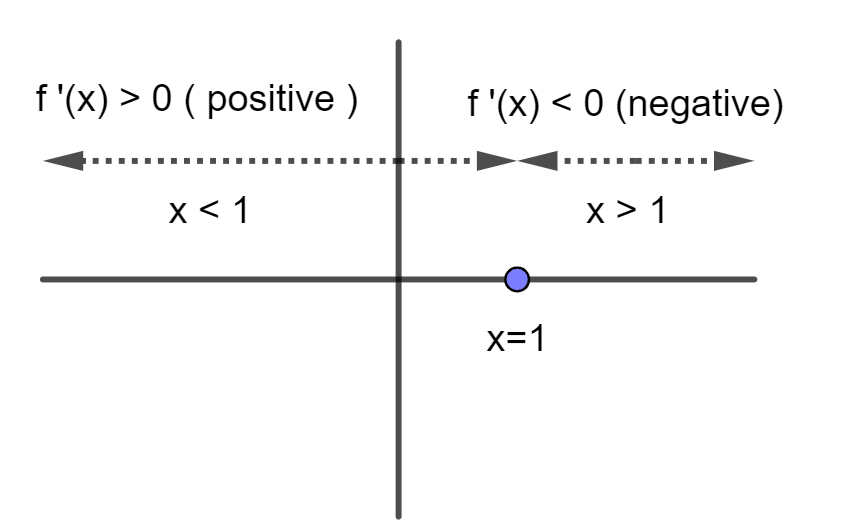
Figure $\left( 1 \right)$ : Nature of function $f'\left( x \right)$ when $x \succ 1{\text{ and }}x < 1$
Now, let us check our options one by one;
$\left( 1 \right)$ Strictly increases in the interval $\left( {\dfrac{1}{2},2} \right)$
This condition is clearly not true since for $x > 1$ the function $f'\left( x \right)$ is negative means decreasing.
$\left( 2 \right)$ Increases in the interval $\left( {0,\infty } \right)$
This condition is also not true as our function is positive for $x < 1$ , drops to zero at $x = 1$ and then decreases from $x \succ 1$ .
$\left( 3 \right)$ Decreases in the interval $\left( {0,2} \right)$
This is clearly not true as we can see from the figure that for $x >1$ the function starts decreasing , the critical point is one not zero for this function.
$\left( 4 \right)$ Strictly decreases in the interval $\left( {1,\infty } \right)$
This option is true since our function $f'\left( x \right) < 0$ means strictly decreasing ${\text{for }}x > 1$ onwards .
Therefore, the correct answer for this question is option $\left( 4 \right)$ .

Note: There can be some confusion about increasing or decreasing and strictly increasing or strictly decreasing functions and what exactly does the term strictly means. If there is a function $y = f\left( x \right)$ then this function is said to be increasing when the value of $y$ increases with increase in the value of $x$ i.e. they can have a positive gradient (slope) or a zero gradient (no change in value of $y$ as value of $x$ changes ) . On the other hand, strictly increasing functions always have a positive gradient, although they can have a zero gradient provided that the zero gradient acts as an inflection point ( where the function changes its sign) .