Question

Select the correct option(s):

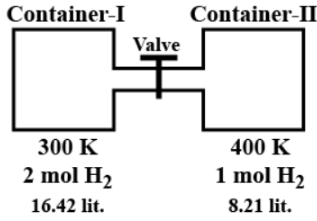
This question has multiple correct options
(A) Pressure in container-I is $3{\text{ atm}}$ before opening the valve.
(B) Pressure after opening the valve is $3.57{\text{ atm}}$ .
(C) Moles in each compartment are the same after opening the valve.
(D) Pressure in each compartment is the same after opening the valve.

Answer 1

Calculate the pressure in container-I and container-II using the ideal gas equation. Use the values given in the question. In equilibrium, the pressure and temperature will be the same in both the containers. Finally, calculate the pressure after the valve is opened and check the options that apply.

Complete answer:
We need to calculate the pressure in each container before opening the valve. To calculate pressure, we will use the ideal gas equation.
$PV = nRT$
Where, $P \to$ pressure of gas
$V \to$ volume of gas
$n \to$ number of moles of gas
$R \to$ universal gas constant $= 0.0821L{\text{ }}atm{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$
$T \to$ temperature of gas
To calculate pressure, we need to manipulate the above equation as follows:
$P = \dfrac{{nRT}}{V}$
For container-I, let ${P_1}$ the pressure, ${V_1}$ be the volume, ${n_1}$ be the no of moles and ${T_1}$ be the temperature. Thus,
${P_1} = \dfrac{{{n_1}R{T_1}}}{{{V_1}}}$
${P_1} = \dfrac{{2 \times 0.0821 \times 300}}{{16.42}}$
On calculating further, we get,
${P_1} = 3{\text{ atm}}$
This proves that option A is correct.
Similarly, for container-II:
${P_2} = \dfrac{{{n_2}R{T_2}}}{{{V_2}}}$
${P_2} = \dfrac{{1 \times 0.0821 \times 400}}{{8.21}}$
${P_2} = 4{\text{ atm}}$
After the valve is opened, the gas inside the containers will try to reach equilibrium. Hence, pressure and temperature will be the same in both the containers.
Thus, option D is also correct.
Let the final temperature after equilibrium be ${T_f}$ , then,
${T_f} = \dfrac{{{n_1}{T_1} + {n_2}{T_2}}}{{{n_1} + {n_2}}}$
On substituting values,
${T_f} = \dfrac{{2 \times 300 + 1 \times 400}}{{2 + 1}}$
${T_f} = \dfrac{{600 + 400}}{3}$
On further solving,
${T_f} = \dfrac{{1000}}{3} = 333.33K$
Hence, the final temperature after the valve is opened is $333.33K$ .
Now, let the final pressure be ${P_f}$ , then,
${P_f} = \dfrac{{({n_1} + {n_2})R{T_f}}}{{({V_1} + {V_2})}}$
${P_f} = \dfrac{{(2 + 1) \times 0.0821 \times 333.33}}{{(16.42 + 8.21)}}$
On simplifying,
${P_f} = \dfrac{{3 \times 0.0821 \times 333.33}}{{24.63}}$
${P_f} = \dfrac{{3 \times 0.0821 \times 333.33}}{{24.63}} = 3.33{\text{ atm}}$
Hence, pressure after the valve is opened is $3.33{\text{ atm}}$ .
Thus, option B is incorrect.
Therefore, the correct options are A and D.

Note:
Option C is incorrect because, after equilibrium, the no of moles in each compartment will not be the same. While solving the equations, use the value of gas constant $R$ as per the units used in question as the value changes when different units are used. For example, the value of $R$ is $8.3145J{K^{ - 1}}mo{l^{ - 1}}$ and $1.9872cal{K^{ - 1}}mo{l^{ - 1}}$ .