Question
Question: If f (x): [1, 3] → [-1,1] satisfies $\int_{1}^{3} f(x)dx = 0$, then the maximum value of $\int_{1}^{...
If f (x): [1, 3] → [-1,1] satisfies ∫13f(x)dx=0, then the maximum value of ∫13xf(x)dx is
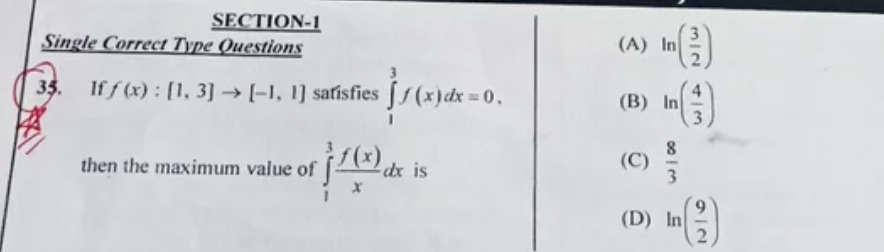
ln(23)
ln(34)
38
ln(29)
ln(34)
Solution
Let I=∫13xf(x)dx. We are given that f(x):[1,3]→[−1,1] and ∫13f(x)dx=0.
We want to maximize I. The integrand is xf(x). The term x1 is a positive and decreasing function on the interval [1,3]. To maximize the integral, we should make f(x) as large as possible (i.e., f(x)=1) where x1 is large (i.e., for small values of x), and f(x) as small as possible (i.e., f(x)=−1) where x1 is small (i.e., for large values of x).
This suggests that the maximizing function f(x) should be of the form:
f(x)=1 for x∈[1,a]
f(x)=−1 for x∈(a,3]
for some value a∈[1,3].
We must satisfy the condition ∫13f(x)dx=0.
∫13f(x)dx=∫1a1dx+∫a3(−1)dx=[x]1a+[−x]a3
=(a−1)+(−3−(−a))=(a−1)+(a−3)=2a−4.
Setting the integral to 0, we get 2a−4=0, which implies a=2.
Since a=2 is in the interval [1,3], this function is valid.
The function is f0(x)={1−1if 1≤x≤2if 2<x≤3.
This function satisfies f0(x)∈[−1,1] for all x∈[1,3] and ∫13f0(x)dx=0.
Now, let's calculate the value of the integral I for this function f0(x):
I0=∫13xf0(x)dx=∫12x1dx+∫23x−1dx
I0=[ln∣x∣]12−[ln∣x∣]23
I0=(ln2−ln1)−(ln3−ln2)
I0=(ln2−0)−(ln3−ln2)
I0=ln2−ln3+ln2=2ln2−ln3=ln(22)−ln3=ln4−ln3=ln(34).
