Question

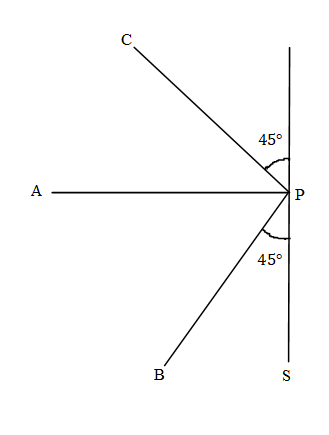
Screen S is illuminated by two point sources A and B. Another source C sends a parallel beam of light towards points P on the screen. Line AP is normal to the screen and the lines AP, BP and CP are 6,3 and 3m respectively. The radiant powers of sources A and B are 45 and 90W respectively. The beam from C is of intensity $0.4\dfrac{{\text{W}}}{{{m^2}}}$. The total incident intensity at P is:

Answer 1

The intensity is defined as the power transferred per unit area. Power is the energy of the striking light. If intensity is more than it means that the power of the striking light is more and the area at which it is striking is less.

Formula used:
The formula of the intensity is equal to,
$\Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta$ is the angle at which the light is striking on the screen.

Complete step by step solution:
It is given in the problem that Screen S is illuminated by two point sources A and B another source C sends a parallel beam of light towards points P on the screen line AP is normal to the screen and the lines AP, BP and CP are 6,3 and 3m respectively. The radiant powers of sources A and B are 45 and 90W respectively the beam from C is of intensity $0.4\dfrac{{\text{W}}}{{{m^2}}}$ and we need to know the total incident intensity at P.
The total intensity at screen is equal to,
$\Rightarrow I = {I_A} + {I_B} + {I_C}$
The light from point A is striking at angle $\theta = 0^\circ$.
The formula of the intensity is equal to,
$\Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta$ is the angle at which the light is striking on the screen.
The power from point A is 45W and AP is equal to 6m.
The intensity ${I_A}$ is equal to,
$\Rightarrow {I_A} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$\Rightarrow {I_A} = \dfrac{{45 \times \cos 0}}{{4\pi \times {6^2}}}$
$\Rightarrow {I_A} = \dfrac{{45 \times 1}}{{4\pi \times 36}}$
$\Rightarrow {I_A} = 0.0995\dfrac{{\text{W}}}{{{m^2}}}$
The intensity from source B,
The formula of the intensity is equal to,
$\Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta$ is the angle at which the light is striking on the screen.
The angle at which the light strikes the screen is$\theta = 45^\circ$, the power is equal to 90W and r=3m.
$\Rightarrow {I_B} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$\Rightarrow {I_B} = \dfrac{{90 \times \cos 45^\circ }}{{4\pi \times {3^2}}}$
$\Rightarrow {I_B} = \dfrac{{90 \times \dfrac{1}{{\sqrt 2 }}}}{{4\pi \times 9}}$
$\Rightarrow {I_B} = 0.563\dfrac{{\text{W}}}{{{m^2}}}$
The intensity for the source is equal to,
The formula of the intensity is equal to,
$\Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta$ is the angle at which the light is striking on the screen.
The intensity of source at point C is equal to$0.4\dfrac{{\text{W}}}{{{m^2}}}$.
$\Rightarrow {I_C} = 0.4\dfrac{{\text{W}}}{{{m^2}}}$.
The total intensity is equal to$I$.
$\Rightarrow I = {I_A} + {I_B} + {I_C}$
$\Rightarrow I = 0.0995 + 0.563 + 0.4$
$\Rightarrow I = 1.0625\dfrac{{\text{W}}}{{{m^2}}}$

The total intensity on the screen is equal $1.0625\dfrac{{\text{W}}}{{{m^2}}}$.

Note: The students are advised to remember the formula of the intensity as it is very useful in solving the problems like these. The intensity of the light is proportional to the cosine of angle of incident on the screen.