Question

Sand is piled up on a horizontal ground in the form of a regular cone of a fixed base radius $R$. The coefficient of static friction between sand layers is $\mu$. The maximum volume of sand that can be pilled up, without the sand slipping on the surface is
A. $\dfrac{{\mu {R^3}}}{{3\pi }}$
B. $\dfrac{{\mu {R^3}}}{3}$
C. $\dfrac{{\pi {R^3}}}{{3\mu }}$
D. $\dfrac{{\mu \pi {R^3}}}{3}$

Answer 1

As the sand gets piled up as a circular cone, we will use the free body diagram to find the relation between forces. Using the angle of friction of the sand particles, we will formulate expressions and then compare them to get the result.

Complete step by step answer:
A circular cone of base radius $R$ is given. Let the height of the cone is $h$. Let $\theta$ be the angle between the slant height and radius. The free body diagram shows the force acting on a sand particle, say $P$.

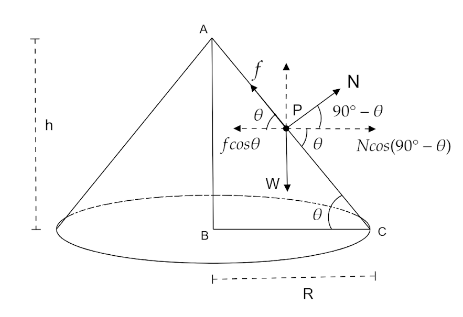
From the horizontal components of force we get,
$f\cos \theta = N\cos ({90^ \circ } - \theta ) = N\sin \theta$
Therefore, dividing both sides by $\cos \theta$ we get,
$f = N\tan \theta$
Now we know that friction is equal to the product of the coefficient of friction and normal.
Substituting $f = \mu N$ in the above equation we get,
$\mu N = N\tan \theta$
Eliminating $N$ from both sides of equation we get,
$\mu = \tan \theta - - - - - \left( 1 \right)$
From geometry with the help from $\Delta$ABC we get,
$\tan \theta = \dfrac{h}{R} - - - - - \left( 2 \right)$
Comparing equation $\left( 1 \right)$ and $\left( 2 \right)$ we get,
$\mu = \dfrac{h}{R}$
$\Rightarrow h = \mu R - - - - - \left( 3 \right)$
Now the maximum volume of the cone $V = \dfrac{1}{3}\pi {R^2}h - - - - \left( 4 \right)$
Substituting $\left( 3 \right)$ in equation $\left( 4 \right)$ we get,
$V = \dfrac{1}{3}\pi {R^2} \times \mu R \\\ \therefore V= \dfrac{{\mu \pi {R^3}}}{3}$

So, the correct option is D.

Note: It must be noted that when a particle on a horizontal plane is slipping then $\mu < \tan \theta$, but when it just slips then $\mu = \tan \theta$.This is also known as limiting value of coefficient of friction. The friction on the surface is the force which restricts the movement of the particles. We must neglect all the other frictional forces working on the sand like air resistance and others.