Question
Question: Same current ‘I’ is flowing in the three infinitely long wire along positive x, y and z directions. ...
Same current ‘I’ is flowing in the three infinitely long wire along positive x, y and z directions. The magnetic field at a point (0, 0, -a) would be:
A. 2πaμ0i(j−i)B. 2πaμ0i(i+j)C. 2πaμ0i(i−j)D. 2πaμ0i(i+j+k)
Solution
First locate point (0, 0, -a) and then apply magnetic field formula along X, Y and Z axis. This will give us the solution for the three infinitely long wires along the 3 – axis given in the question.
Formula used:
B=2πrμoI
Complete step by step solution:
First let’s locate point A (0, 0, -a) on the axis as shown in the figure.
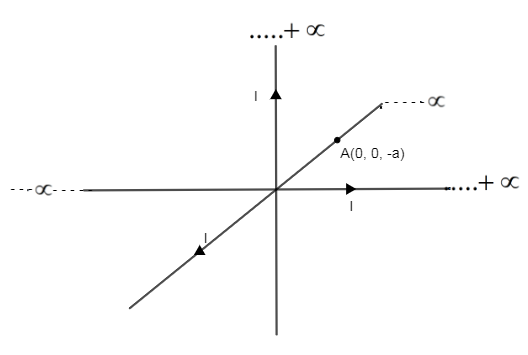
As we can say in the figure point A is located on the -Z- axis
Current directions are in +Z -axis as shown in the figure.
Now the magnitude field at point A is,
BA=BX+BY+BZ...(1)
Where, BA = magnetic field at point A.
BX= magnetic field due to X- axis
BY= magnetic field due to Y-axis
BZ= magnetic field due to Z-axis
Now let’s findBX,
Formula for the magnetic field is,
⇒B=2πrμoI
Where, B = magnetic field
μo= Permeability of the free space
r = distance from the wire to the point.
Here r will be taken as ‘a’ for BX
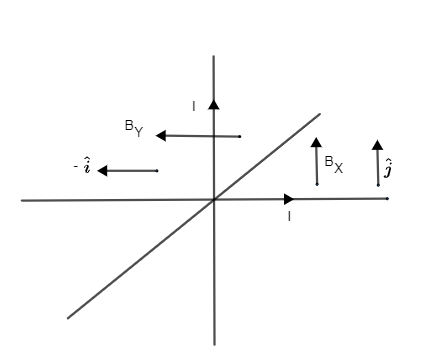
BX=(2πaμoI)j
Direction of BXis in j direction.
Now similarly,
BY=(2πaμoI)(−i)
Direction of BYwill be (−i)direction.
Now, BZwill be zero because the point A (0, 0, -a) lies on the Z-axis itself.
BZ=O
Now let’s put all the values in equation (1)
⇒BA=(2πaμoI)j+(2πaμoI)i+o∴BA=(2πaμoI)(j−i)
Hence the correct option is (A) (2πaμoI)(j−i),
Note:
When we are giving direction for the magnitude fields don’t mistake directions given for i as BX because it is in the X direction use the thumb rule for the direction of the magnetic field as shown in figure.
