Question
Question: $S_n = \frac{1}{2.4} + \frac{1.3}{2.4.6} + \frac{1.3.5}{2.4.6.8} + ...$ ...
Sn=2.41+2.4.61.3+2.4.6.81.3.5+...
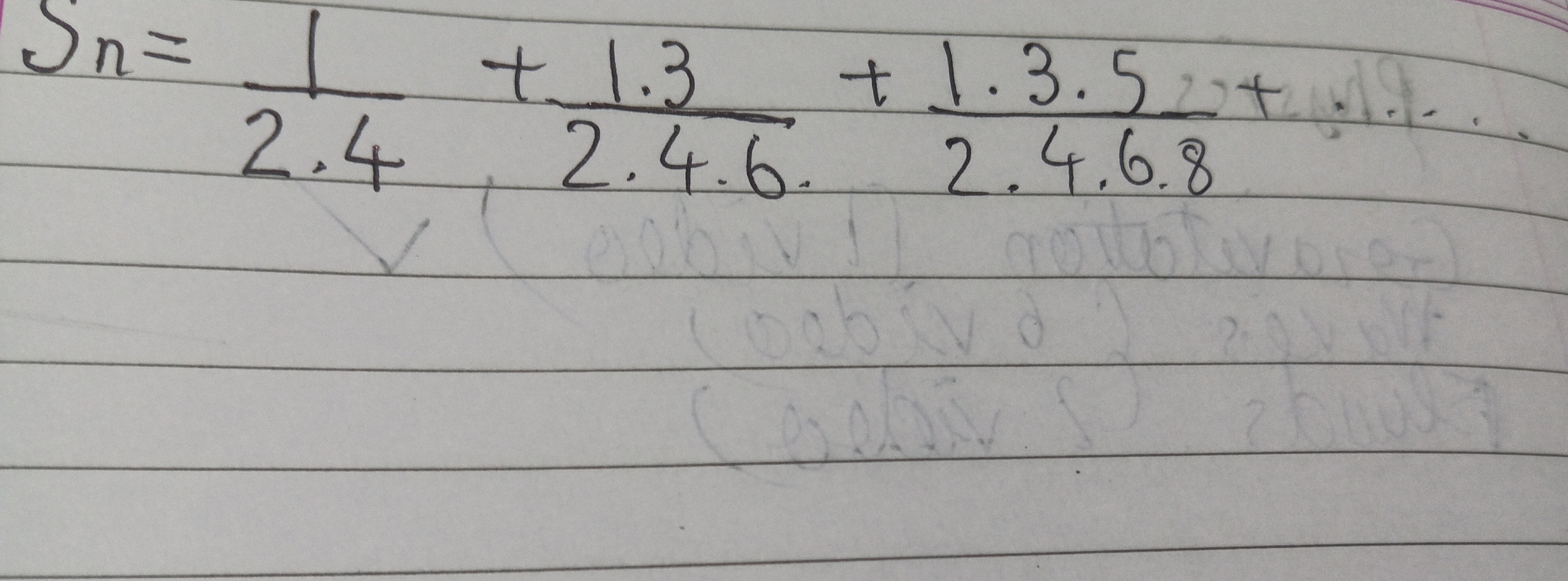
1/2
Solution
The given series is Sn=2.41+2.4.61.3+2.4.6.81.3.5+...
Let's write the general term of the series, Tk.
The numerator of the k-th term (for k≥1) is the product of the first k odd numbers: 1⋅3⋅5⋅⋯⋅(2k−1).
The denominator of the k-th term is the product of the first k+1 even numbers: 2⋅4⋅6⋅⋯⋅(2k+2).
So, Tk=2⋅4⋅6⋅⋯⋅(2k+2)1⋅3⋅5⋅⋯⋅(2k−1).
We can rewrite the numerator and denominator using factorials.
Numerator: 1⋅3⋅5⋅⋯⋅(2k−1)=2⋅4⋅⋯⋅(2k)(2k)!=2kk!(2k)!.
Denominator: 2⋅4⋅6⋅⋯⋅(2k+2)=2k+1(1⋅2⋅3⋅⋯⋅(k+1))=2k+1(k+1)!.
So, the k-th term Tk is:
Tk=2k+1(k+1)!2kk!(2k)!=2kk!⋅2k+1(k+1)!(2k)!=22k+1k!(k+1)!(2k)!
We know that (k2k)=k!k!(2k)!.
So, Tk=22k+11k+11k!k!(2k)!=22k+11k+11(k2k).
Tk=2⋅4k1k+11(k2k).
The sum Sn (which is an infinite series, let's call it S) is:
S=∑k=1∞Tk=∑k=1∞2⋅4k1k+11(k2k).
S=21∑k=1∞k+11(k2k)(41)k.
This series is related to the generating function for Catalan numbers. The k-th Catalan number is Ck=k+11(k2k).
The generating function for Catalan numbers is given by:
G(x)=∑k=0∞Ckxk=∑k=0∞k+11(k2k)xk.
It is a known result that G(x)=2x1−1−4x.
We need to evaluate the sum ∑k=1∞k+11(k2k)(41)k.
This sum is G(41) excluding the k=0 term.
The k=0 term of G(x) is C0x0=0+11(00)(x0)=1⋅1⋅1=1.
So, ∑k=1∞k+11(k2k)(41)k=G(41)−C0.
Let's substitute x=41 into G(x):
G(41)=2(41)1−1−4(41)=211−1−1=211−0=211=2.
Now, substitute this back into the expression for S:
S=21(G(41)−C0)=21(2−1)=21(1)=21.
The sum of the series is 21.
