Question
Question: If $\sin^{-1}(x^2 - 4x + 5) + \cos^{-1}(y^2 - 2y + 2) = \pi / 2$, then:...
If sin−1(x2−4x+5)+cos−1(y2−2y+2)=π/2, then:
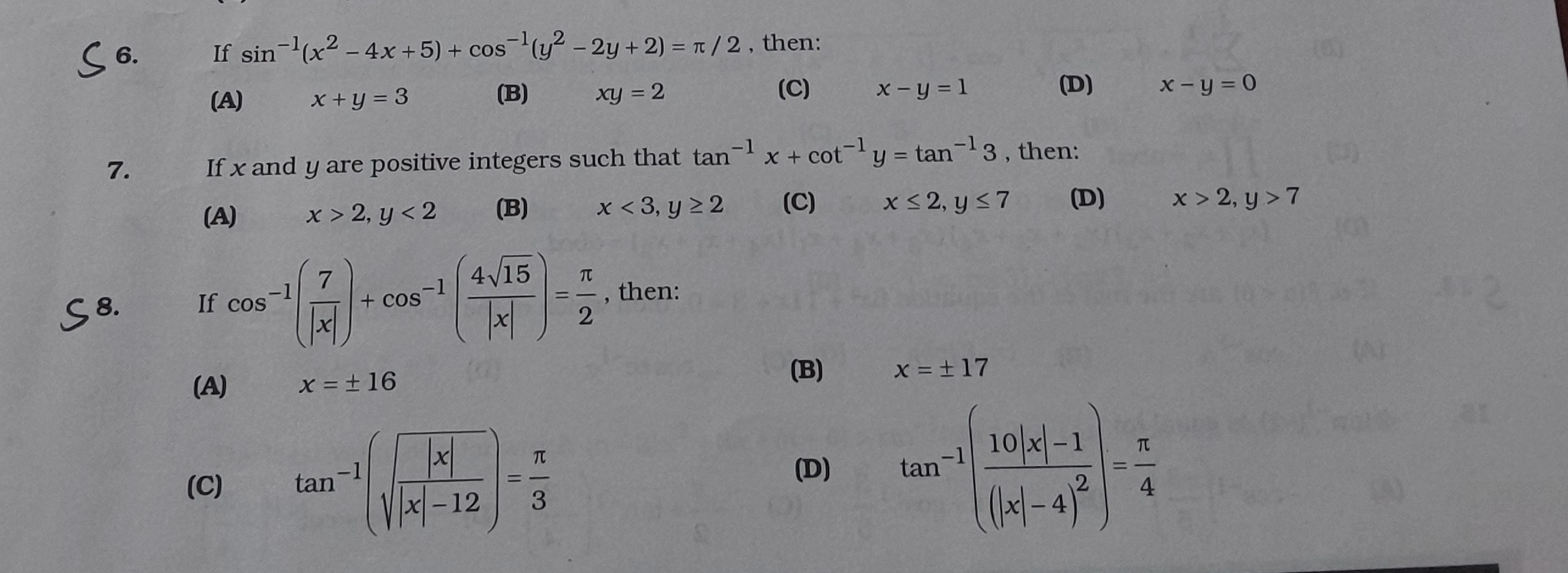
x+y=3
xy=2
x−y=1
x−y=0
A, B, C
Solution
The given equation is sin−1(x2−4x+5)+cos−1(y2−2y+2)=π/2.
For sin−1(A) and cos−1(B) to be defined, their arguments must be in the interval [−1,1]. Let's analyze the arguments:
-
x2−4x+5: This expression can be rewritten by completing the square: x2−4x+5=(x2−4x+4)+1=(x−2)2+1. Since (x−2)2≥0 for all real x, we have (x−2)2+1≥1. For sin−1((x−2)2+1) to be defined, we must have (x−2)2+1∈[−1,1]. The only value in [−1,1] that is also ≥1 is 1. Therefore, (x−2)2+1=1, which implies (x−2)2=0. This gives x−2=0, so x=2.
-
y2−2y+2: This expression can be rewritten by completing the square: y2−2y+2=(y2−2y+1)+1=(y−1)2+1. Since (y−1)2≥0 for all real y, we have (y−1)2+1≥1. For cos−1((y−1)2+1) to be defined, we must have (y−1)2+1∈[−1,1]. The only value in [−1,1] that is also ≥1 is 1. Therefore, (y−1)2+1=1, which implies (y−1)2=0. This gives y−1=0, so y=1.
Thus, the only possible values are x=2 and y=1. Now we check the given options with x=2 and y=1: (A) x+y=2+1=3. This statement is true. (B) xy=2×1=2. This statement is true. (C) x−y=2−1=1. This statement is true. (D) x−y=0. This statement is false, as 2−1=1=0.
Since the question asks "then:", it implies which of the given statements are true. All options (A), (B), and (C) are true.
