Question

Find the sum of the series $S = 1 + \frac{2^2}{3^2} + \frac{6^2}{4^2} + \dots$ up to $n$ terms.

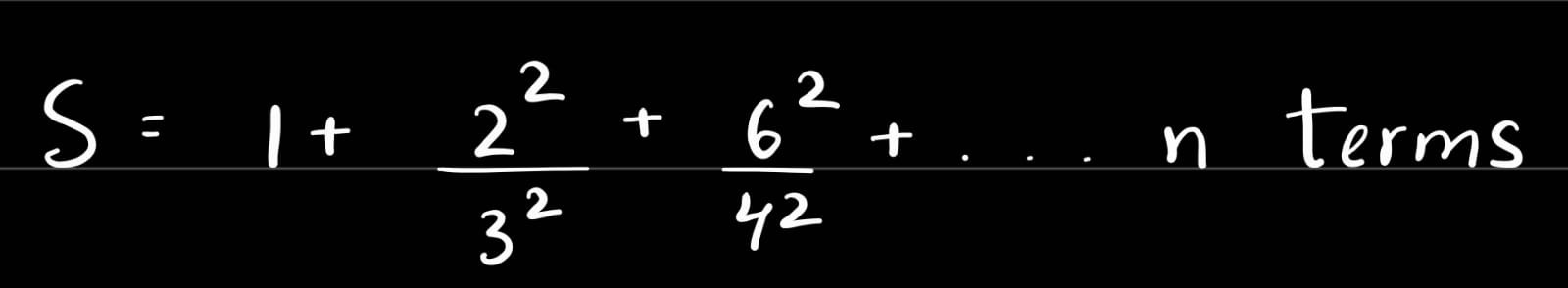
Answer 1

$S = 1 \;+\;\sum_{k=2}^{n}\frac{(k!)^{2}}{(k+1)^{2}}$

Answer 2

Step 1. Recognize the $k$th term.
For $k\ge2$, the numerator follows $2,6,24,\dots$ i.e.\ $k!$. Hence the $k$th term is

$$T_{k} \;=\;\frac{(k!)^{2}}{(k+1)^{2}}\quad (k\ge2)$$

with $T_{1}=1$.

Step 2. Write the partial sum.

$$S_{n} = T_{1} + \sum_{k=2}^{n}T_{k} = 1 + \sum_{k=2}^{n}\frac{(k!)^{2}}{(k+1)^{2}}.$$

No simpler closed form in elementary terms exists beyond this factorial summation.