Question
Question: S₁ = $\sum_{r=1}^{n}r$, S₂ = $\sum_{r=1}^{n}r^2$ and S₃ = $\sum_{r=1}^{n}r^3$, then the value of $\l...
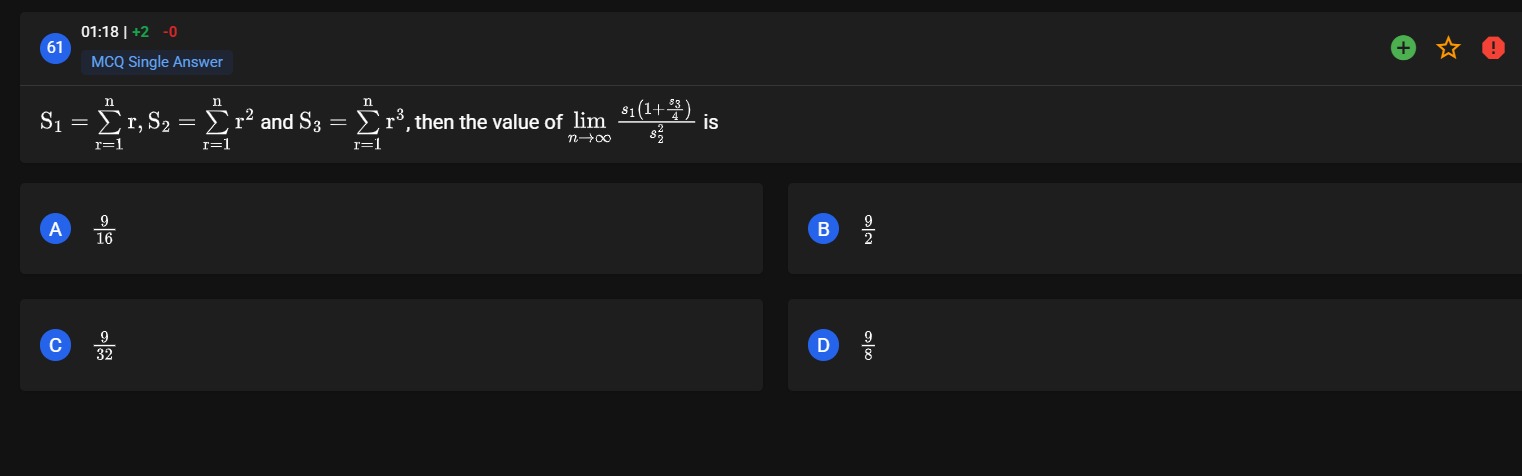
S₁ = ∑r=1nr, S₂ = ∑r=1nr2 and S₃ = ∑r=1nr3, then the value of limn→∞s22s1(1+4s3) is
A
169
B
29
C
329
D
89
Answer
329
Explanation
Solution
For large n, we use the asymptotic formulas:
S1S2S3=r=1∑nr≈2n2,=r=1∑nr2≈3n3,=r=1∑nr3≈(2n2)2=4n4.The given expression is:
n→∞limS22S1(1+4S3).Substitute the asymptotic values:
1+4S3≈1+16n4∼16n4(since 16n4≫1).Now, the numerator becomes:
S1(1+4S3)∼2n2⋅16n4=32n6.And the denominator:
S22∼(3n3)2=9n6.Thus, the limit is:
n→∞lim9n632n6=329.