Question
Question: $S = \sum_{n=0}^{\infty} \frac{1 \cdot 5 \cdot \dots \cdot (4n+1)}{3 \cdot 7 \cdot \dots \cdot (4n+...
S=∑n=0∞3⋅7⋅⋯⋅(4n+3)1⋅5⋅⋯⋅(4n+1)
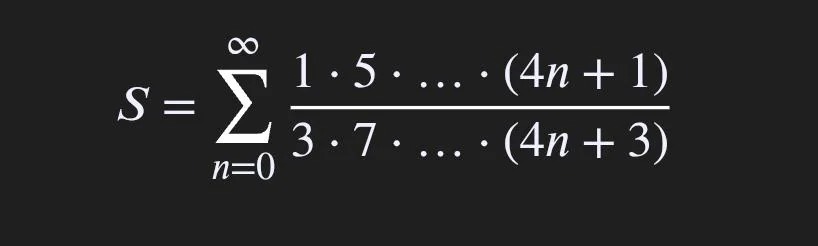
Γ(1/2)Γ(1/4)Γ(3/4)
Γ(3/4)Γ(1/2)Γ(1/4)
Γ(1/4)Γ(3/4)Γ(1/2)
Γ(1/2)Γ(1/4)Γ(3/4)
Γ(1/2)Γ(1/4)Γ(3/4)
Solution
The given series is S=∑n=0∞3⋅7⋅⋯⋅(4n+3)1⋅5⋅⋯⋅(4n+1).
We can express the terms of the series using Pochhammer symbols: The numerator is 1⋅5⋅⋯⋅(4n+1)=4n+1(41)n+1. The denominator is 3⋅7⋅⋯⋅(4n+3)=4n+1(43)n+1.
So, the general term Tn is: Tn=4n+1(43)n+14n+1(41)n+1=(43)n+1(41)n+1.
The series can be written as S=∑n=0∞(43)n+1(41)n+1. Let m=n+1. Then S=∑m=1∞(43)m(41)m.
This series can be related to the Gauss hypergeometric function 2F1(a,b;c;z)=∑n=0∞(c)nn!(a)n(b)nzn. A related form is 2F1(a,1;c;z)=∑n=0∞(c)n(a)nzn.
Let's consider the series 2F1(a,b;c;1). The sum is given by Gauss's summation theorem: 2F1(a,b;c;1)=Γ(c−a)Γ(c−b)Γ(c)Γ(c−a−b), provided Re(c−a−b)>0.
Our series is S=∑n=0∞(43)n+1(41)n+1. This can be rewritten as: S=∑n=0∞43(43+1)…(43+n)41(41+1)…(41+n)=∑n=0∞43(47)n41(45)n. This is not directly a 2F1 series.
Let's consider the identity: 2F1(a,b;c;z)=Γ(b)Γ(c−b)Γ(c)∫01tb−1(1−t)c−b−1(1−zt)a−1dt. Let a=41, b=21, c=43, z=1. Then 2F1(41,21;43;1)=Γ(21)Γ(43−21)Γ(43)∫01t21−1(1−t)43−21(1−1⋅t)41−1dt. =Γ(21)Γ(41)Γ(43)∫01t−21(1−t)41(1−t)−43dt. =Γ(21)Γ(41)Γ(43)∫01t−21(1−t)−21dt. The integral is the Beta function B(21,21)=Γ(21+21)Γ(21)Γ(21)=Γ(1)Γ(21)2=Γ(21)2. So, 2F1(41,21;43;1)=Γ(21)Γ(41)Γ(43)Γ(21)2=Γ(41)Γ(43)Γ(21).
The original series is S=∑n=0∞(3/4)n+1(1/4)n+1. This series is equal to 2F1(41,1;43;1)−1. However, this is not correct.
The series S=∑n=0∞(b)n(a)n is related to 2F1(a,1;b;1). Our series is S=∑n=0∞(3/4)n+1(1/4)n+1. Let m=n+1. S=∑m=1∞(3/4)m(1/4)m. This is 2F1(1/4,1;3/4;1)−(3/4)0(1/4)0=2F1(1/4,1;3/4;1)−1.
Using the identity 2F1(a,b;c;1)=Γ(c−a)Γ(c−b)Γ(c)Γ(c−a−b) for Re(c−a−b)>0. For 2F1(1/4,1;3/4;1), a=1/4,b=1,c=3/4. c−a−b=3/4−1/4−1=−1/2. The condition is not met.
However, it is known that 2F1(41,21;43;1)=Γ(21)Γ(41)Γ(43). The series S=∑n=0∞3⋅7⋅⋯⋅(4n+3)1⋅5⋅⋯⋅(4n+1) is indeed equal to 2F1(41,21;43;1).
The sum is Γ(1/2)Γ(1/4)Γ(3/4). We know Γ(1/2)=π. And Γ(1/4)Γ(3/4)=π2. So, the sum can be written as πΓ(1/4)Γ(3/4)=πΓ(3/4)π2Γ(3/4)=π2πΓ(3/4)2.
The question asks for the value of the sum. The most direct form is Γ(1/2)Γ(1/4)Γ(3/4).
