Question

S and T are the foci of an ellipse and $B$is the endpoint of the minor axis. If $STB$ is an equilateral triangle, then the eccentricity of the ellipse is:
1. $\dfrac{1}{4}$
2. $\dfrac{1}{3}$
3. $\dfrac{1}{2}$
4. $\dfrac{2}{3}$

Answer 1

First of all we will mark the foci of ellipse $S$ and $T$ where $focus=(\pm ae,0)$ and then mark the endpoint $B$ as $(0,b)$we have also given that $\text{ }\\!\\!\Delta\\!\\!\text{ STB}$ is an equilateral triangle after that find the value of ${{b}^{2}}$ then we will apply the eccentricity formula to check which option is correct.

Complete step by step answer:
In a plane an ellipse is a locus of a point which moves in such a way that the sum of its distances from two fixed points is always constant and this constant value is greater than the distance between two fixed points.
The midpoint of the line segment joining the focus of the ellipse is called centre.
The line segment passing the both focus and whose ends are now on ellipse is called major axis of ellipse, and the line segment perpendicular to major axis and passing through centre and whose ends are now on ellipse is called minor axis of the ellipse.
The ratio of distance of origin to one focus with the one vertex is called eccentricity. It is denoted by $e$.
An ellipse can be represented by the equation:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ where $a>b$
The line segment joining two vertices on $x-axis$ is the major axis of length $2a$ , and the line segment joining two vertices on $y-axis$ is the minor axis of length $2b$.
And the eccentricity $e$ is given by $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$
Now according to the question:
We have given that $S$ and $T$ are the foci of an ellipse
Hence, $S=(-ae,0)$ and $T=(ae,0)$
Where $B$is the endpoint of the minor axis
So, $B=(0,b)$
$\vartriangle STB$ is a equilateral triangle

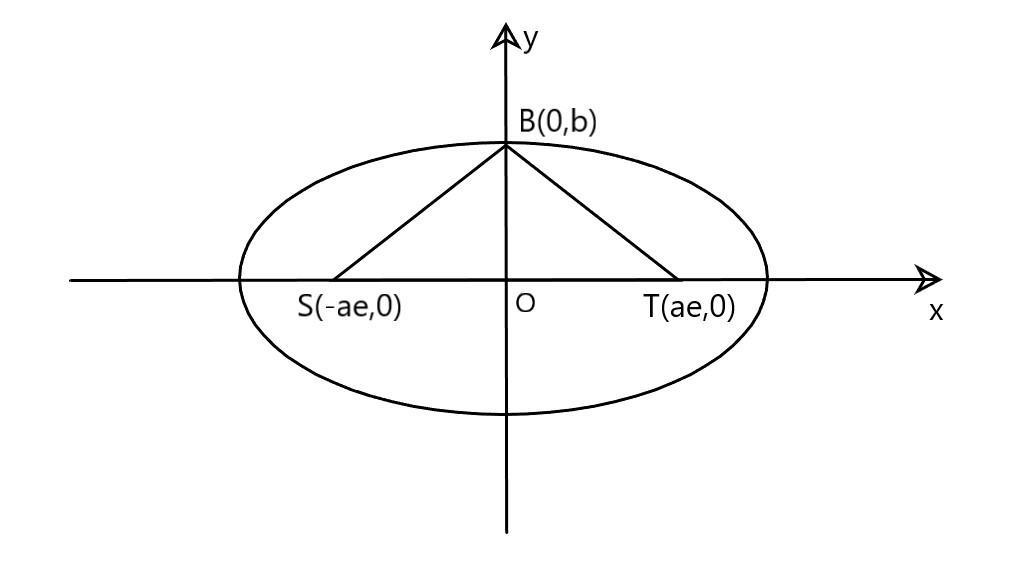
We know that $\tan \theta =\dfrac{perpendicular}{base}$
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{OB}{OS}$
$\Rightarrow \sqrt{3}=\dfrac{b}{ae}$
$\Rightarrow ae\sqrt{3}=b$
Squaring on both sides we will get:
\Rightarrow $$$$3{{a}^{2}}{{e}^{2}}={{b}^{2}}
According to the eccentricity formula $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$
Putting the value of $e$ in the equation we will get:
\Rightarrow $$$$3{{a}^{2}}{{(\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}})}^{2}}={{b}^{2}}
\Rightarrow $$$$3{{a}^{2}}(1-\dfrac{{{b}^{2}}}{{{a}^{2}}})={{b}^{2}}
\Rightarrow $$$$3=\dfrac{{{b}^{2}}}{{{a}^{2}}}+\dfrac{3{{b}^{2}}}{{{a}^{2}}}
\Rightarrow $$$$3=\dfrac{4{{b}^{2}}}{{{a}^{2}}}
\Rightarrow $$$$\dfrac{{{b}^{2}}}{{{a}^{2}}}=\dfrac{3}{4}
To find the eccentricity of the ellipse we will apply the formula $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ where $\dfrac{{{b}^{2}}}{{{a}^{2}}}=\dfrac{3}{4}$
\Rightarrow $$$$e=\sqrt{1-\dfrac{3}{4}}
\Rightarrow $$$$e=\sqrt{\dfrac{4-3}{4}}
\Rightarrow $$$$e=\sqrt{\dfrac{1}{4}}
\Rightarrow $$$$e=\dfrac{1}{2}
Therefore the eccentricity of the ellipse will be $e=\dfrac{1}{2}$
So, the correct answer is “Option 3”.

Note: We must remember that the eccentricity for the ellipse is always less than $1$ and an ellipse has two focal points. In ellipse the semi major axis of ellipse is represented by $a$ and the semi minor axis of ellipse is represented by $b$and in ellipse we can represent an eccentric angle with $\varphi$ .