Question

S 9. $\lim_{x \to a} \left\{\left[\frac{a^{1/2}+x^{1/2}}{a^{1/4}-x^{1/4}}\right]^{-1}-\frac{2(ax)^{1/4}}{x^{3/4}-a^{1/4}x^{1/2}+a^{1/2}x^{1/4}-a^{3/4}}\right\}^{-\sqrt{2}^{\log_4 a}}$

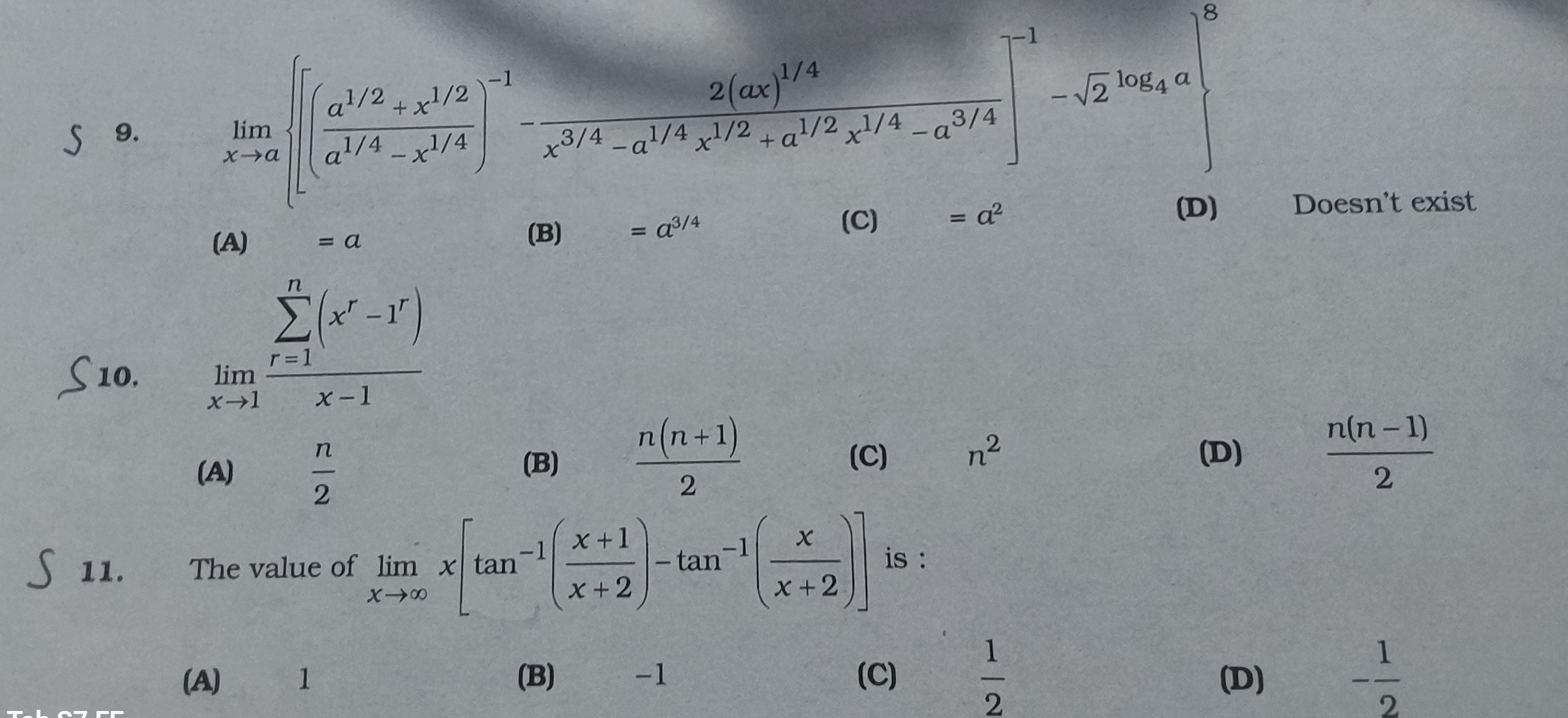
• A. = a
• B. = $a^{3/4}$
• C. = $a^2$
• D. Doesn't exist

Answer 1

Answer: (D)

Doesn't exist

Answer 2

Solution:

Let the given expression be $L$. We need to evaluate: $L = \lim_{x \to a} \left\{\left[\frac{a^{1/2}+x^{1/2}}{a^{1/4}-x^{1/4}}\right]^{-1}-\frac{2(ax)^{1/4}}{x^{3/4}-a^{1/4}x^{1/2}+a^{1/2}x^{1/4}-a^{3/4}}\right\}^{-\sqrt{2}^{\log_4 a}}$

First, let's simplify the expression inside the curly braces. Let $A = a^{1/4}$ and $X = x^{1/4}$. Then $a^{1/2} = A^2$, $x^{1/2} = X^2$, $a^{3/4} = A^3$, $x^{3/4} = X^3$. The expression inside the curly braces becomes: $\left[\frac{A^2+X^2}{A-X}\right]^{-1} - \frac{2(AX)}{X^3-AX^2+A^2X-A^3}$

Simplify the first term: $\left[\frac{A^2+X^2}{A-X}\right]^{-1} = \frac{A-X}{A^2+X^2}$

Simplify the denominator of the second term by factoring by grouping: $X^3-AX^2+A^2X-A^3 = X^2(X-A) + A^2(X-A) = (X^2+A^2)(X-A)$

Now substitute these back into the expression inside the curly braces: $\frac{A-X}{A^2+X^2} - \frac{2AX}{(X^2+A^2)(X-A)}$ $= \frac{-(X-A)}{A^2+X^2} - \frac{2AX}{(X^2+A^2)(X-A)}$ To combine these terms, find a common denominator, which is $(X^2+A^2)(X-A)$: $= \frac{-(X-A)(X-A) - 2AX}{(X^2+A^2)(X-A)}$ $= \frac{-(X-A)^2 - 2AX}{(X^2+A^2)(X-A)}$ Expand $(X-A)^2 = X^2-2AX+A^2$: $= \frac{-(X^2-2AX+A^2) - 2AX}{(X^2+A^2)(X-A)}$ $= \frac{-X^2+2AX-A^2-2AX}{(X^2+A^2)(X-A)}$ $= \frac{-X^2-A^2}{(X^2+A^2)(X-A)}$ $= \frac{-(X^2+A^2)}{(X^2+A^2)(X-A)}$ $= \frac{-1}{X-A}$

Substitute back $X = x^{1/4}$ and $A = a^{1/4}$: The expression inside the curly braces simplifies to $\frac{-1}{x^{1/4}-a^{1/4}}$.

Now, let's simplify the exponent: $-\sqrt{2}^{\log_4 a}$ We know that $\log_4 a = \frac{\log_2 a}{\log_2 4} = \frac{\log_2 a}{2}$. So, $-\sqrt{2}^{\log_4 a} = -(2^{1/2})^{\frac{\log_2 a}{2}} = -2^{\frac{1}{2} \cdot \frac{1}{2} \log_2 a} = -2^{\frac{1}{4} \log_2 a}$ Using the property $b^{\log_b k} = k$, we have $2^{\frac{1}{4} \log_2 a} = 2^{\log_2 (a^{1/4})} = a^{1/4}$. Thus, the exponent is $-a^{1/4}$.

Now, the limit becomes: $L = \lim_{x \to a} \left[\frac{-1}{x^{1/4}-a^{1/4}}\right]^{-a^{1/4}}$

Let $h = x^{1/4}-a^{1/4}$. As $x \to a$, $h \to 0$. The expression becomes: $L = \lim_{h \to 0} \left[\frac{-1}{h}\right]^{-a^{1/4}}$

For $a>0$, $a^{1/4}$ is a positive real number. As $h \to 0^+$, $\frac{-1}{h} \to -\infty$. So the base approaches $-\infty$. As $h \to 0^-$, $\frac{-1}{h} \to +\infty$. So the base approaches $+\infty$.

Case 1: $h \to 0^+$ $L_1 = \lim_{h \to 0^+} \left[\frac{-1}{h}\right]^{-a^{1/4}} = (-\infty)^{-a^{1/4}}$ If $-a^{1/4} < 0$, which it is since $a^{1/4}>0$, then $(-\infty)^{-a^{1/4}} = \frac{1}{(-\infty)^{a^{1/4}}}$. If $a^{1/4}$ is a positive integer, then $L_1 = 0$. If $a^{1/4}$ is not an integer, the expression is not defined in real numbers for a negative base.

Case 2: $h \to 0^-$ $L_2 = \lim_{h \to 0^-} \left[\frac{-1}{h}\right]^{-a^{1/4}} = (+\infty)^{-a^{1/4}}$ If $-a^{1/4} < 0$, then $(+\infty)^{-a^{1/4}} = \frac{1}{(+\infty)^{a^{1/4}}} = 0$.

Since the limit from the left and right are not necessarily equal (due to the sign of the base for non-integer exponents) or the expression is undefined for real numbers, the limit is considered to not exist. Even if we consider cases where it might be 0, the options are $a$, $a^{3/4}$, $a^2$, or "Doesn't exist". Given the standard context of such problems, if the limit approaches different values or is undefined from different sides, or involves operations with infinity that are not well-defined, the limit is considered to not exist.

The only way for the limit to be one of the options (A), (B), (C) is if the base does not go to infinity or the exponent allows for a finite non-zero value, which is not the case here.

Therefore, the limit does not exist.