Question

Let $f(n) = \sum_{\substack{k=-n \\ k\neq 0}}^{n} (cot^{-1}(\frac{1}{k}) - tan^{-1}(k))$ such that $\sum_{n=2}^{10} (f(n)+f(n-1)) = a\pi$ then find the value of $(a + 1)$.

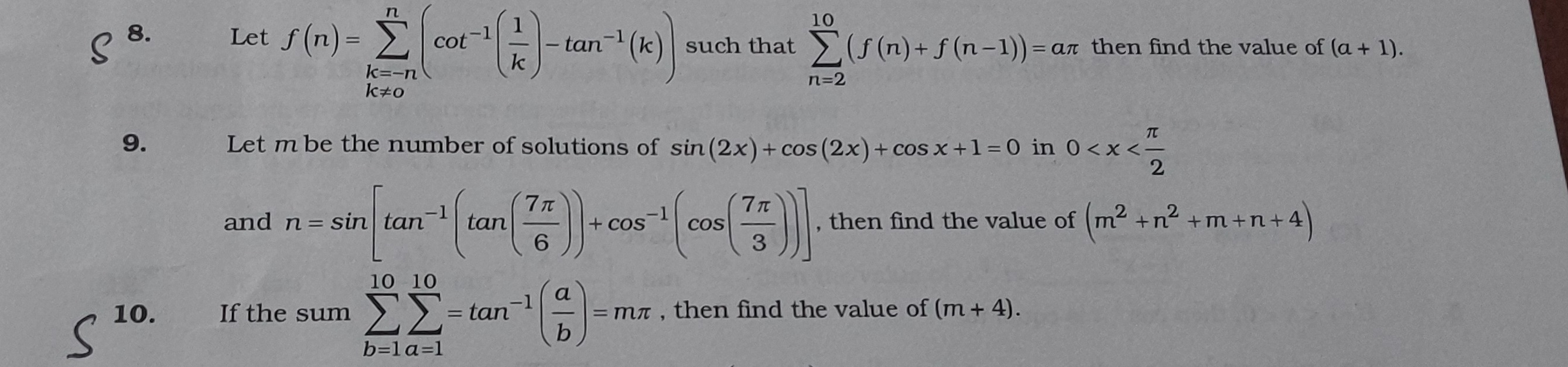
Answer 1

100

Answer 2

1. Term $cot^{-1}(\frac{1}{k}) - tan^{-1}(k)$ is $0$ if $k>0$, and $\pi$ if $k<0$.
2. $f(n) = \sum_{k=1}^n 0 + \sum_{k=-n}^{-1} \pi = n\pi$.
3. $\sum_{n=2}^{10} (f(n)+f(n-1)) = \sum_{n=2}^{10} (n\pi + (n-1)\pi) = \sum_{n=2}^{10} (2n-1)\pi$.
4. $\sum_{n=2}^{10} (2n-1) = (2(2)-1) + (2(3)-1) + \dots + (2(10)-1) = 3+5+\dots+19$. This is an A.P. with 9 terms. Sum $= \frac{9}{2}(3+19) = \frac{9}{2}(22) = 99$.
5. So, $\sum_{n=2}^{10} (f(n)+f(n-1)) = 99\pi$.
6. Given $a\pi = 99\pi \implies a=99$.
7. $(a+1) = 99+1 = 100$.