Question
Question: $\lim_{x \to -\infty} \frac{x^5 \tan(\frac{1}{\pi x^2})+3|x|^2+7}{|x|^3+7|x|+8}$...
limx→−∞∣x∣3+7∣x∣+8x5tan(πx21)+3∣x∣2+7
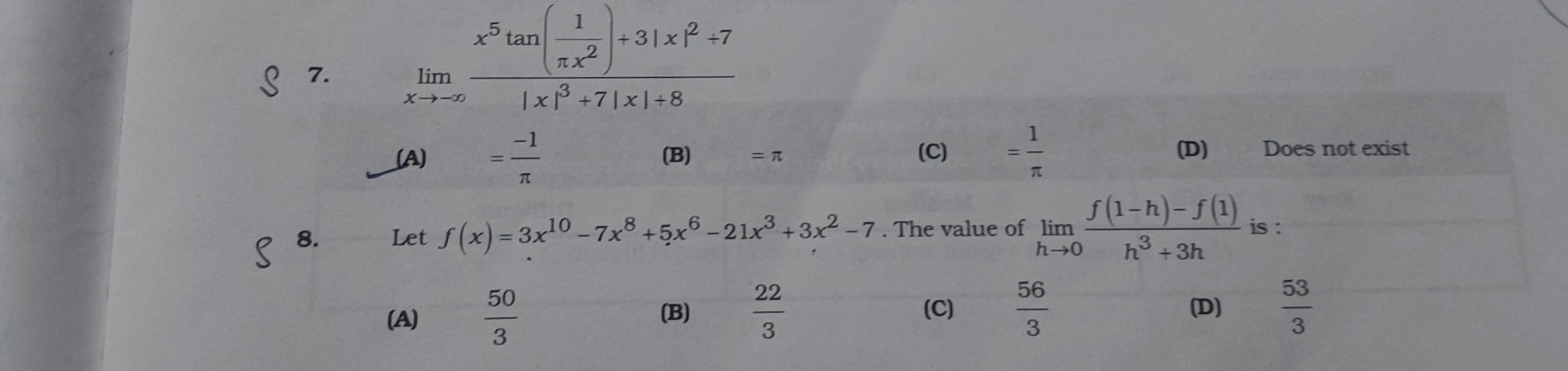
A
= π−1
B
= π
C
= π1
D
Does not exist
Answer
= π−1
Explanation
Solution
For x→−∞, ∣x∣=−x.
limx→−∞−x3−7x+8x5tan(πx21)+3x2+7
As x→−∞, πx21→0. Using tany≈y for small y:
x5tan(πx21)≈x5⋅πx21=πx3.
The limit becomes limx→−∞−x3−7x+8πx3+3x2+7.
Divide numerator and denominator by x3:
limx→−∞−1−x27+x38π1+x3+x37=−1−0+0π1+0+0=−π1.
