Solveeit Logo
Login

Question

Question: If $x = \sin^{-1}(a^6+1)+\cos^{-1}(a^4+1)-\tan^{-1}(a^2+1), a \in R$, then the value of $\sec^2 x$ i...

If x=sin⁡−1(a6+1)+cos⁡−1(a4+1)−tan⁡−1(a2+1),a∈Rx = \sin^{-1}(a^6+1)+\cos^{-1}(a^4+1)-\tan^{-1}(a^2+1), a \in R, then the value of sec⁡2x\sec^2 x is 2.

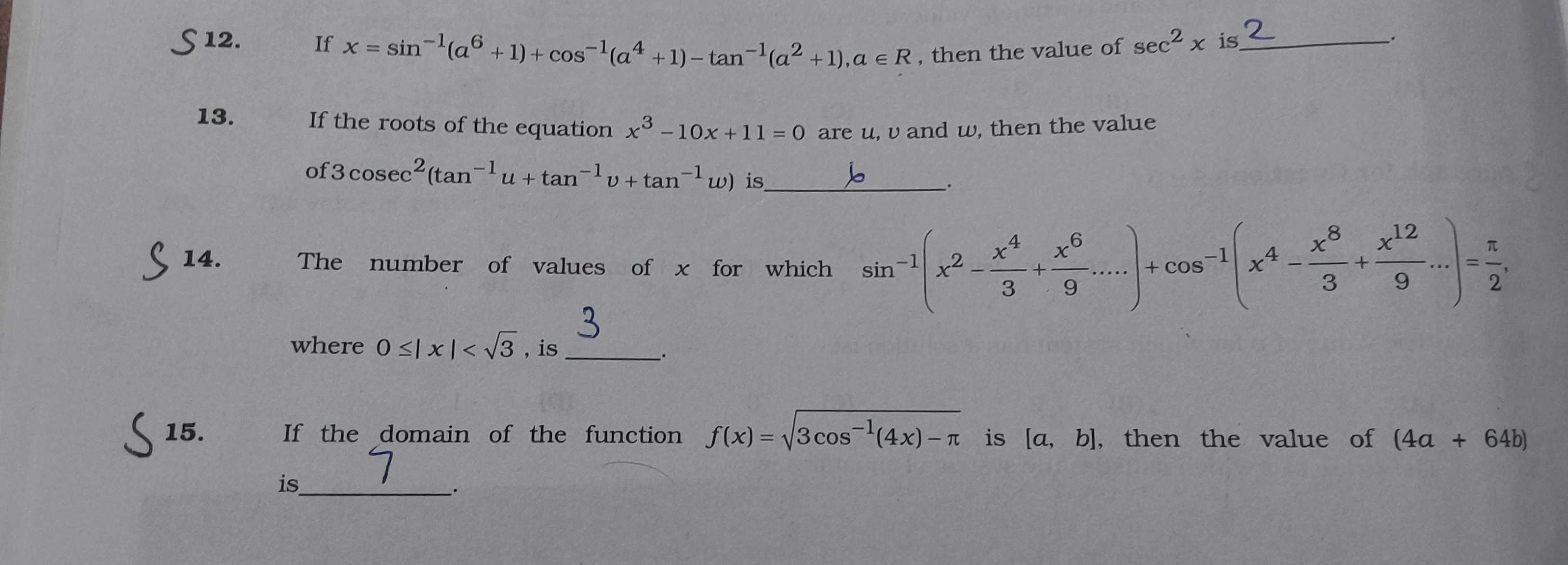
Answer

True

Explanation

Solution

For sin⁡−1(a6+1)\sin^{-1}(a^6+1) and cos⁡−1(a4+1)\cos^{-1}(a^4+1) to be defined, a6+1=1a^6+1=1 and a4+1=1a^4+1=1, both implying a=0a=0.
Substitute a=0a=0 into the expression for xx to get x=sin⁡−1(1)+cos⁡−1(1)−tan⁡−1(1)=π2+0−π4=π4x = \sin^{-1}(1)+\cos^{-1}(1)-\tan^{-1}(1) = \frac{\pi}{2}+0-\frac{\pi}{4}=\frac{\pi}{4}.
Then sec⁡2x=sec⁡2(π4)=(2)2=2\sec^2 x = \sec^2(\frac{\pi}{4}) = (\sqrt{2})^2 = 2.