Question

The least and greatest values of $(\sin^{-1}x)^3 + (\cos^{-1}x)^3$ are respectively:

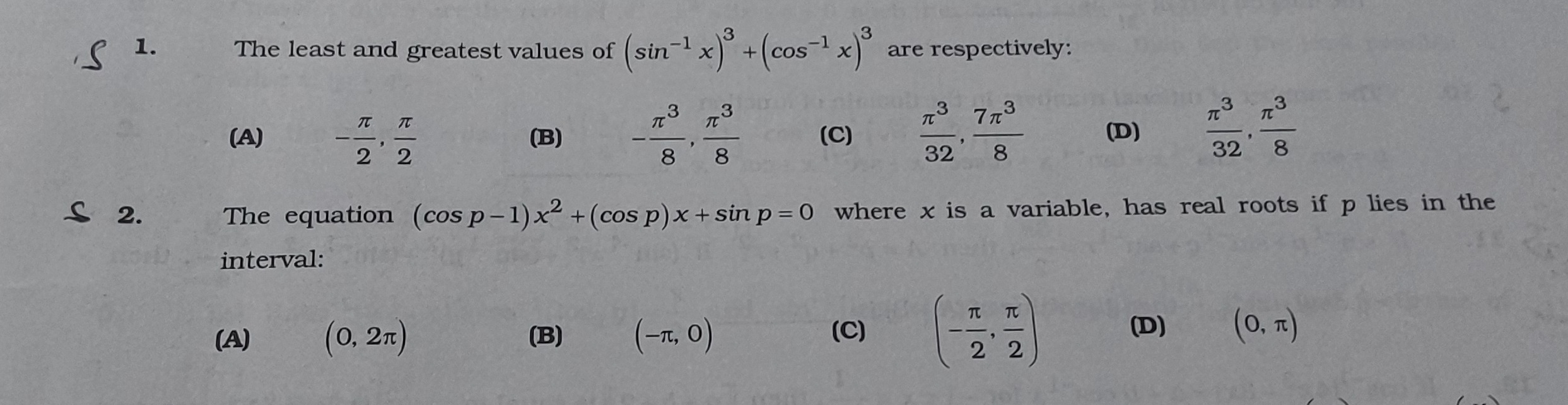
• A. $-\frac{\pi}{2}, \frac{\pi}{2}$
• B. $-\frac{\pi^3}{8}, \frac{\pi^3}{8}$
• C. $\frac{\pi^3}{32}, \frac{7\pi^3}{8}$
• D. $\frac{\pi^3}{32}, \frac{\pi^3}{8}$

Answer 1

Answer: (C)

(C)

Answer 2

Let $a = \sin^{-1}x$. Then $\cos^{-1}x = \frac{\pi}{2} - a$. The expression becomes $y = a^3 + (\frac{\pi}{2} - a)^3$.

Expand this as $y = \frac{\pi}{2}(3a^2 - \frac{3\pi}{2}a + \frac{\pi^2}{4})$.

The domain for $a$ is $[-\frac{\pi}{2}, \frac{\pi}{2}]$.

This is a quadratic in $a$ opening upwards. Its vertex is at $a = \frac{\pi}{4}$.

Evaluate $y$ at the vertex $a=\frac{\pi}{4}$ and endpoints $a=-\frac{\pi}{2}, a=\frac{\pi}{2}$.

At $a=\frac{\pi}{4}$, $y = \frac{\pi^3}{32}$ (minimum).

At $a=-\frac{\pi}{2}$, $y = \frac{7\pi^3}{8}$ (maximum).

At $a=\frac{\pi}{2}$, $y = \frac{\pi^3}{8}$.

The least value is $\frac{\pi^3}{32}$ and the greatest value is $\frac{7\pi^3}{8}$.