Question

${{S}_{1}}$ and ${{S}_{2}}$ are the two coherent point sources of light located in the XY plane at points $(0,0)$ and $(0,3\lambda )$ respectively. Here $\lambda$ is the wavelength of the light. At which one of the following points (given as coordinates), the intensity of interference will be maximum?
A. $(3\lambda ,0)$
B. $(4\lambda ,0)$
C. $\left( {}^{5\lambda }/{}_{4} , 0\right)$
D. $\left( {}^{2\lambda }/{}_{3} , 0\right)$

Answer 1

In this question we are asked to calculate the maximum intensity of interference. We know that the intensity of light will be maximum if the light reaching from path 1 and 2 is equal to $\lambda$. Therefore, using this concept we will first calculate the path difference between the light and equate the path difference with condition for maximum intensity.

Formula used:
$\Delta x={{S}_{2}}P-{{S}_{1}}P$

Complete answer:
We know that, at point P the intensity would be maximum if the light from path 1 and path 2 is equal to $\lambda$. Therefore,
From the diagram given below, we can say path difference in between the light is given by,

               ![](https://www.vedantu.com/question-sets/a3ab1e03-319a-46da-93fe-eb010aec5a296201448115983352400.png)   

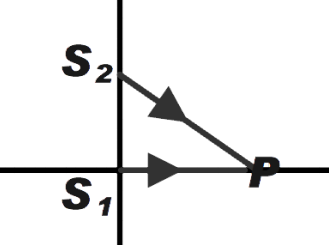
$\Delta x={{S}_{2}}P-{{S}_{1}}P$ ……………….. (1)
Where ${{S}_{1}}$ and ${{S}_{2}}$ are the distances.
From the diagram given above we can say that
${{S}_{1}}P=(x-0)-(0-0)=x$
Similarly ${{S}_{2}}P$ can be given as
${{S}_{2}}P=\sqrt{{{(0-x)}^{2}}+{{(3\lambda -0)}^{2}}}$
${{S}_{2}}P=\sqrt{{{x}^{2}}+9{{\lambda }^{2}}}$
After substituting the calculated values in equation (1)
We get,
$\Delta x=\sqrt{{{x}^{2}}+9{{\lambda }^{2}}}-{{x}^{2}}$
Now we know that for maximum intensity
$\Delta x=\lambda$
Therefore, we can say that
$\lambda =\sqrt{{{x}^{2}}+9{{\lambda }^{2}}}-{{x}^{2}}$
Therefore,
${{x}^{2}}+9{{\lambda }^{2}}={{x}^{2}}+{{y}^{2}}+2\lambda x$
On solving,
We get,
$x=\dfrac{8{{\lambda }^{2}}}{2\lambda }$
$x=4\lambda$
Therefore, the coordinates would be $(4\lambda ,0)$

So, the correct answer is “Option B”.

Note:
The path difference is basically the distance travelled by two waves from their respective sources. It is used to describe the difference in degrees or radians When two or more alternating quantities reach their maximum high or zero. The intensity of interference is the difference between two waves.