Question

The standard EMF of the cell in which the reaction, $MnO_4^- + 5Fe^{2+} + 8H^+ \rightarrow Mn^{2+} + 5Fe^{3+} + 4H_2O$ occurs is 0.59 V at 25°C. The log of equilibrium constant for the given reaction is approximately?

Answer 1

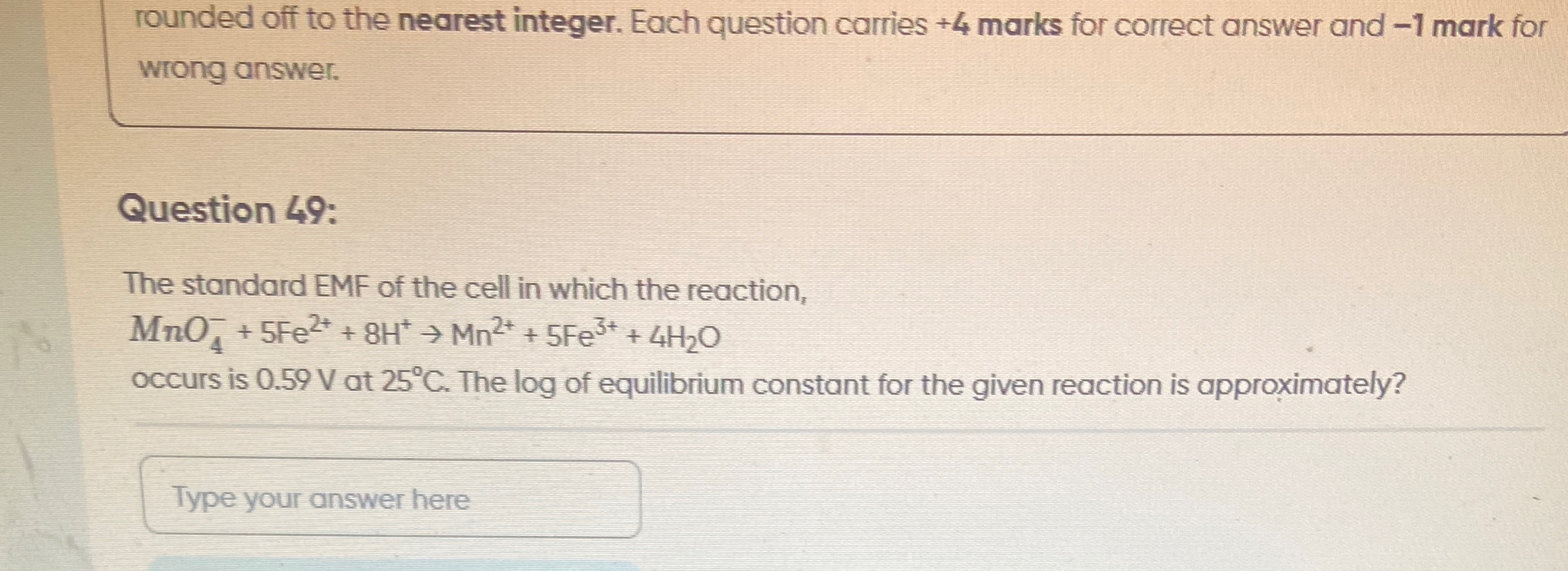
50

Answer 2

The relationship between the standard EMF ($E^\circ_{cell}$) and the equilibrium constant (K) of a reaction at 25°C is given by the Nernst equation at equilibrium:

$E^\circ_{cell} = \frac{0.0591}{n} \log K$

First, determine the number of electrons (n) involved in the given reaction: $MnO_4^- + 5Fe^{2+} + 8H^+ \rightarrow Mn^{2+} + 5Fe^{3+} + 4H_2O$

1. Oxidation state change for Mn: In $MnO_4^-$, Mn is in the +7 oxidation state. In $Mn^{2+}$, Mn is in the +2 oxidation state. The change is from +7 to +2, which means a gain of 5 electrons ($MnO_4^- + 5e^- \rightarrow Mn^{2+}$). This is a reduction half-reaction.

2. Oxidation state change for Fe: In $Fe^{2+}$, Fe is in the +2 oxidation state. In $Fe^{3+}$, Fe is in the +3 oxidation state. The change is from +2 to +3, which means a loss of 1 electron ($Fe^{2+} \rightarrow Fe^{3+} + e^-$). This is an oxidation half-reaction.

To balance the electrons lost and gained, 5 moles of $Fe^{2+}$ must be oxidized for every 1 mole of $MnO_4^-$ reduced. Thus, the total number of electrons (n) transferred in the balanced reaction is 5.

Given: Standard EMF ($E^\circ_{cell}$) = 0.59 V Number of electrons (n) = 5 Temperature = 25°C

Substitute the values into the Nernst equation: $0.59 = \frac{0.0591}{5} \log K$

Now, solve for $\log K$: $\log K = \frac{0.59 \times 5}{0.0591}$ $\log K = \frac{2.95}{0.0591}$ $\log K \approx 49.91539$

Rounding off to the nearest integer, $\log K$ is approximately 50.

Explanation of the solution:

The Nernst equation at equilibrium, $E^\circ_{cell} = \frac{0.0591}{n} \log K$, relates the standard cell potential ($E^\circ_{cell}$) to the equilibrium constant (K) and the number of electrons (n) transferred. For the given reaction, the oxidation state change of Mn from +7 to +2 indicates a gain of 5 electrons, and the oxidation state change of Fe from +2 to +3 indicates a loss of 1 electron. To balance the electron transfer, 5 $Fe^{2+}$ ions are oxidized for every $MnO_4^-$ ion reduced, so n=5. Substituting $E^\circ_{cell} = 0.59$ V and n=5 into the equation yields $\log K = \frac{0.59 \times 5}{0.0591} \approx 49.915$, which rounds to 50.