Question

Rod ${\text{A}}$ can slide in a vertical direction pushing the triangular wedge $B$ towards right. The wedge is moving toward right with uniform acceleration ${{\text{a}}_{\text{B}}}$ . Find acceleration of the rod ${\text{A}}$ .

Answer 1

According to the question, the acceleration of the wedge towards the right side is given as ${{\text{a}}_{\text{B}}}$ . The rod $A$ is fixed and hence, it cannot move towards the right side. It can only move downwards as shown in the figure below.

Complete Step-by-Step Solution

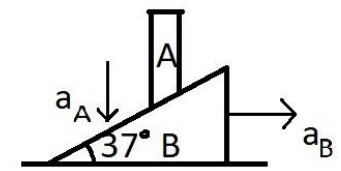
The acceleration of the wedge $B$ towards right hand side is given as ${{\text{a}}_{\text{B}}}$
Let us suppose the acceleration of rod a in the downwards direction as ${a_A}$
Now, we have to find out the point of contact of the rod with the wedge
After finding out the point of contact of the rod with wedge, we will draw the stick figure of the point of contact as per the figure below

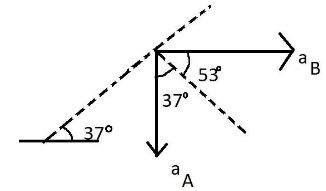
We will also determine the angles at which the various forces are acting by using simple mathematics and concepts of right-angled triangle and opposite angles.
After drawing the stick figure of all the forces and their components that can be determined, we can conclude that
${a_A}\cos {37^ \circ } = {a_B}\cos {53^ \circ }$
Now we will substitute the values of $\cos {37^ \circ }$ and $\cos {53^ \circ }$ in the above equation to get
${a_A}\dfrac{4}{5} = {a_B}\dfrac{3}{5}$
Rearranging the above equation, we can obtain the value of acceleration ${a_A}$ as
${a_A} = \dfrac{3}{4}{a_B}$
Therefore, our final answer is ${a_A} = \dfrac{3}{4}{a_B}$ .

Note
Acceleration, since it has both magnitude and direction, is a vector quantity. It is also the second position derivative with respect to time, or it is the first velocity derivative with respect to time. Acceleration is defined as the rate of change of velocity with respect to time. In circular motion, speed remains constant, but since the direction changes, the velocity changes, and the body is said to be accelerated.