Question
Question: $\frac{(x-1)^2(x-3)(x+3)}{(x+4)^3.x(x-3)}>0$...
(x+4)3.x(x−3)(x−1)2(x−3)(x+3)>0
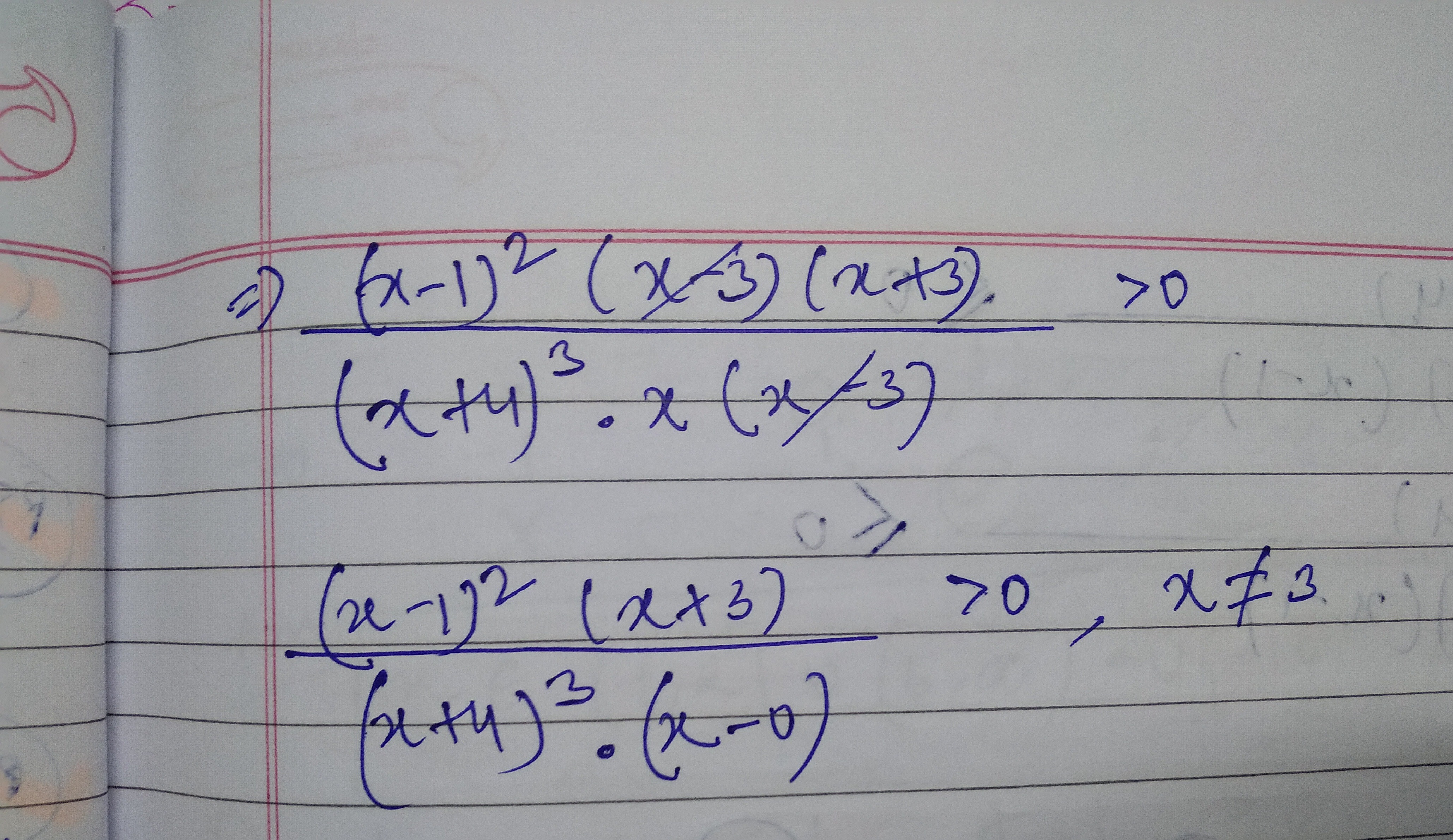
A
(x+4)3.(x−0)(x−1)2(x+3)>0,x=3.
B
The solution set is (−4,−3)∪(0,1)∪(1,3)∪(3,∞).
C
The solution set is (−4,−3)∪(0,3)∪(3,∞).
D
The solution set is (−4,−3)∪(0,∞).
Answer
The solution set is (−4,−3)∪(0,1)∪(1,3)∪(3,∞).
Explanation
Solution
The critical points are x=−4,−3,0,1,3. The expression simplifies to x(x+4)3(x−1)2(x+3) for x=3. We analyze the sign of this expression in the intervals defined by the critical points.
- For x>3, all factors are positive, so the expression is positive.
- For 1<x<3, (x−1)2>0, (x+3)>0, x>0, (x+4)3>0. The expression is positive.
- For 0<x<1, (x−1)2>0, (x+3)>0, x>0, (x+4)3>0. The expression is positive.
- For −3<x<0, (x−1)2>0, (x+3)>0, x<0, (x+4)3>0. The expression is negative.
- For −4<x<−3, (x−1)2>0, (x+3)<0, x<0, (x+4)3>0. The expression is positive.
- For x<−4, (x−1)2>0, (x+3)<0, x<0, (x+4)3<0. The expression is negative. The inequality holds for (−4,−3)∪(0,1)∪(1,3)∪(3,∞).
