Question
Question: $\Rightarrow F' = \frac{1}{2\pi\epsilon_0} \times \frac{qQx}{[(\frac{d}{2})^2 + x^2]^{3/2}}$ For ma...
⇒F′=2πϵ01×[(2d)2+x2]3/2qQx
For maximum force, dxdF′=0
2πϵ0qQ×[[(2d)2+x2]−3/2−x23[(2d)2+x2]−5/22x]=0
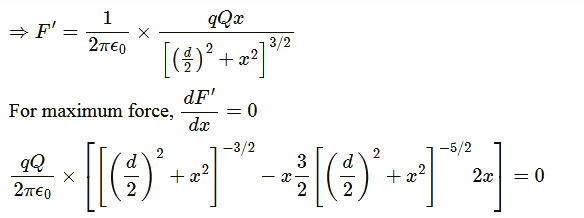
x=±22d
Solution
The given equation is derived from setting the first derivative of the force F′ with respect to x equal to zero to find the condition for maximum force. The equation is: 2πϵ0qQ×[((2d)2+x2)−3/2−x23((2d)2+x2)−5/22x]=0
Since 2πϵ0qQ is a non-zero constant (assuming q,Q=0), we can divide the equation by this term: ((2d)2+x2)−3/2−x23((2d)2+x2)−5/22x=0
Simplify the second term: x23((2d)2+x2)−5/22x=3x2((2d)2+x2)−5/2
The equation becomes: ((2d)2+x2)−3/2−3x2((2d)2+x2)−5/2=0
Factor out the term with the lower power, ((2d)2+x2)−5/2: ((2d)2+x2)−5/2[((2d)2+x2)−5/2((2d)2+x2)−3/2−3x2]=0
Simplify the term inside the square bracket using the rule anam=am−n: ((2d)2+x2)−5/2((2d)2+x2)−3/2=((2d)2+x2)−3/2−(−5/2)=((2d)2+x2)−3/2+5/2=((2d)2+x2)2/2=(2d)2+x2
Substitute this back into the factored equation: ((2d)2+x2)−5/2[(2d)2+x2−3x2]=0
The term ((2d)2+x2)−5/2=((2d)2+x2)5/21 is non-zero for real values of x and d (unless d=0 and x=0, where the original force is undefined). Therefore, the term in the square bracket must be zero: (2d)2+x2−3x2=0
Combine the x2 terms: (2d)2−2x2=0
Solve for x2: 4d2=2x2 x2=4×2d2 x2=8d2
Take the square root of both sides to find x: x=±8d2 x=±8d x=±22d
The maximum force occurs when the test charge is located at a distance ∣x∣=22d from the origin along the axis.
