Question

Resultant by component method:

Answer 1

Split the vectors along X and Y axis respectively. Then add all the vectors along X-axis and all the vectors along Y-axis. Use the formula to find the resultant vectors.

Complete step by step solution:
Since the $\overline{OA}$ is not parallel to any axes hence we will need to take components of the $\overline{OA}$ along X-axis and Y-axis. The vectors AB and BC are parallel to X-axis and Y-axis respectively. We need to find the component of $\overline{OA}$ in the X and Y direction.

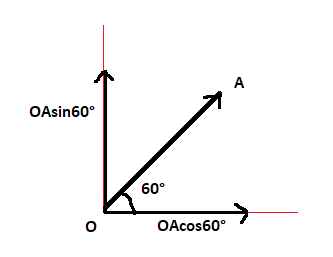
From the above both figures we can have the vectors in both X-axis and Y-axis, since the component of $\overline{OA}$ is now in both axes.
$|{\overrightarrow {OA} _x}| = |OA|\cos {60^ \circ } = 6(\frac{1}{2}) = 3$
$|{\overrightarrow {AB} _x}| = |AB|\cos \theta = 4\cos {0^ \circ } = 4(1) = 4$
|{\overrightarrow {OA} _y}| = |OA|\sin {60^ \circ } = 6(\frac{{\sqrt 3 }}{2}) = 3\sqrt 3 $$$$|{\overrightarrow {OA} _y}| = |OA|\sin {60^ \circ } = 6(\frac{{\sqrt 3 }}{2}) = 3\sqrt 3
$|{\overrightarrow {BC} _y}| = |BC|\sin \theta = 3\sin {90^ \circ } = 3(1) = 3$
Adding all the three vectors along X and Y direction we get
$\overrightarrow{{{P}_{x}}}=\overrightarrow{O{{A}_{x}}}+\overrightarrow{A{{B}_{x}}}+\overrightarrow{B{{C}_{x}}}$ $\overrightarrow{{{P}_{y}}}=\overrightarrow{O{{A}_{y}}}+\overrightarrow{A{{B}_{y}}}+\overrightarrow{B{{C}_{y}}}$
Since we have already calculated the magnitudes of all three vectors, we can easily calculate the magnitude of $\overrightarrow{P}$
$|\overrightarrow{{{P}_{x}}}|=3+4+0=7$
$|\overrightarrow{{{P}_{y}}}|=3\sqrt{3}+0+3=3\sqrt{3}+3$
Now the resultant vector will be as follows:

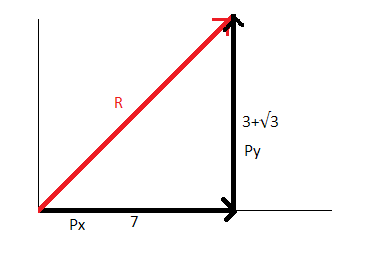
Here we have added all the $3$ vectors in both X direction and Y direction to get the resultant in each direction. Now it is easy to calculate the resultant when $2$ vectors are given. It is to be noted that the angle here between both vectors is ${{90}^{\circ }}$
The resultant will be given as
$\sqrt{{{P}_{x}}^{2}+{{P}_{y}}^{2}+2{{P}_{x}}{{P}_{y}}\cos \theta }$
$\Rightarrow \sqrt{{{7}^{2}}+{{(3\sqrt{3}+3)}^{2}}}$
$\Rightarrow \sqrt{116.1769}$
$\Rightarrow 10.78$

Therefore, the resultant vector has a magnitude of $10.78$.

Note: The resultant of any number of vectors can be found by taking the component of vectors in X and Y direction. Once we have a component of the vector in X and Y direction, we can easily find the resultant by using the above given formula.