Question

Resonant frequency of a LC circuit is 10 kHz. Calculate the value of inductance, if the capacitance is 50μF.

Answer 1

It is given in the question that the LC circuit is at resonance. To find the value of inductance we have to consider a relation between $\omega ,L,C$. We will establish the relation for these terms to solve the given question, adding to the point that the circuit is at resonance.

Complete Step-By-Step answer:
We know that in an LC circuit the capacitor and the inductor will either be in series or in parallel.

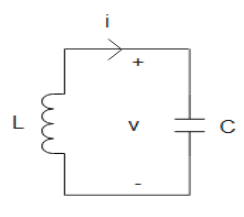
We have been given,

The resonant frequency = 10kHz.
Capacitance = 50μF

To find the value of inductance we will be using the formula,
$\Rightarrow {{X}_{C}}={{X}_{L}}$ ……………, (1)

Capacitive reactance is formulated as,
$\Rightarrow {{X}_{C}}=\dfrac{1}{\omega C}$ …………., (2)
Where,
$\omega$= angular frequency
C = capacitance

Inductive reactance is formulated as,
$\Rightarrow {{X}_{L}}=\omega L$………………., (3)
Where,
L = inductance

Now we will substitute (2) and (3) in (1), we get,
$\Rightarrow \dfrac{1}{\omega C}=\omega L$
$\Rightarrow L=\dfrac{1}{{{\omega }^{2}}C}$ …………………., (4)

But we know that, $\omega =2\pi f$
Where f is the resonance frequency.

Now finding the value of the angular frequency using the formula,
$\omega =2\pi f$
We get,

&\Rightarrow \omega =2\pi (10\times {{10}^{3}}) \\\ &\Rightarrow \omega =2\pi ({{10}^{4}}) \\\ \end{aligned}$$ Now to find the value of inductance we will substitute the value of $$\omega $$ in (4), $\Rightarrow L=\dfrac{1}{{{\omega }^{2}}C}$ $\Rightarrow L=\dfrac{1}{{{(2\pi \times {{10}^{4}})}^{2}}\times 50\times {{10}^{-6}}}$ $\Rightarrow L=\dfrac{1}{4{{\pi }^{2}}\times {{10}^{8}}\times 50\times {{10}^{-6}}}$ $\Rightarrow L=5.07\times {{10}^{-6}}H$ **Hence, the value of inductance is $$L=5.07\times {{10}^{-6}}H$$.** **Note:** It is important for students to remember that in case of an inductor, voltage leads current by an angle of 90 degree. While in the case of a capacitor the current leads the voltage by an angle of 90 degrees. But in a resistor, both the current and the voltage will be in the same phase. It is also important to keep the units of all the parameters in its SI unit, in case this is not followed then the correct answer will not be obtained. LC circuits are used in oscillators, filters and tuners.