Question

Resolve horizontally and vertically a force $F = 8N$ which makes an angle of ${45^0}$ with the horizontal:
A) $\left( {\text{A}} \right){\text{ }}4\sqrt 2 i + 4\sqrt 2 j$ $N$
B) $\left( {\text{B}} \right){\text{ }} - 4\sqrt 2 i + 4\sqrt 2 j$ $N$
C) $\left( {\text{C}} \right){\text{ }}4\sqrt 2 i - 4\sqrt 2 j$ $N$
D) $\left( {\text{D}} \right){\text{ }} - 4\sqrt 2 i - 4\sqrt 2 j$ $N$

Answer 1

-Use the concept of the Resolution of vectors in two rectangular components.
-Since force is a vector quantity it can be divided into two rectangular components i.e the angle between the components is ${90^0}$.
-Hence the force is then the sum of the two components which are along the x-axis and the y-axis can be represented by the unit vectors $i$ and $j$.

Formula used:
The horizontal component of the force $F$ is, ${F_H} = F\cos \theta$
The vertical component of the force $F$ is, ${F_V} = F\sin \theta$
$\overrightarrow F = F\cos \theta i + F\sin \theta j$

Complete step by step answer:
The resolution of vectors states that if a vector is divided into two or more vectors in such a way that the original vector becomes the resultant of these dividend parts. These parts are called the components of the original vector.

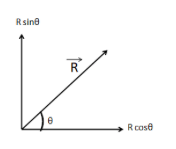
This diagram shows the resolution of the $\overrightarrow R$ vector in rectangular components which are $R\cos \theta$ and $R\sin \theta$ horizontally and vertically respectively. Hence the $\overrightarrow R$ vector can be represented as, $\overrightarrow R = R\cos \theta i + R\sin \theta j$, where $i$ and $j$ are the unit vectors along horizontally and vertically respectively.
Since force is a vector quantity it can be divided into two rectangular components.
Such as,

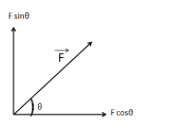
Given, the angle between the horizontal component and the original vector, $\theta$ = ${45^0}$. Since the angle between the components is ${90^0}$. The angle between the original vector and the vertical component is also $\theta$ = ${45^0}$.
The horizontal component of the force $F$ is, ${F_H} = F\cos \theta = F\cos {45^0}$
The vertical component of the force $F$ is, ${F_V} = F\sin \theta = IF\sin {45^0}$
$\overrightarrow F = F\cos \theta i + F\sin \theta j$
$\overrightarrow F = F\cos 4{5^0}i + F\sin 4{5^0}j$
$F$is the modulus of $\overrightarrow F$ = $8N$
$\therefore \overrightarrow F = 8 \times \dfrac{1}{{\sqrt 2 }}i + 8 \times \dfrac{1}{{\sqrt 2 }}j$ [since, $\cos {45^0} = \dfrac{1}{{\sqrt 2 }}{\text{and}}\sin {45^0} = \dfrac{1}{{\sqrt 2 }}$ ]
$\therefore \overrightarrow F = 4\sqrt 2 i + 4\sqrt 2 j$ $$$$
Hence the right answer is in option $\left( A \right)$.

Notes: If we make a component of the $\overrightarrow R$vector along the direction of $\overrightarrow R$, then $R\cos \theta = R\cos 0 = R$and the perpendicular component will be $R\sin \theta = R\sin 0 = 0$.
Hence we may conclude that,
i) The value of the component along the direction of its original vector is the same as the value of the vector.
ii) There is no component perpendicular to the vector.