Question

Represent the following pair of equations graphically and write the coordinates of points where the line intersects the y-axis.
$\begin{aligned} & x+3y=6 \\\ & 2x-3y=12 \\\ \end{aligned}$

Answer 1

Hint: Here, first we have to find the two points to draw the graph of the system of equations $x+3y=6$ and $2x-3y=12$. While choosing the points, first take $x=0$ and then find the value of y. Similarly, for $y=0$, find the value of x. Using the two points of the equations, plot the graph. From the graph identify the points that intersect $x+3y=6$ and $2x-3y=12$ with the y-axis which are the required coordinates.

Complete step-by-step answer:
Here, we are given with the equations:
$\begin{aligned} & x+3y=6 \\\ & 2x-3y=12 \\\ \end{aligned}$
Now, we have to represent the above equations graphically and have to find the coordinates of points where the line intersects the y-axis.
First consider the equation:
$x+3y=6$
Now, we have to draw the line corresponding to the given equation. For that consider two points.
When $x=0$, then the equation,
$\begin{aligned} & \Rightarrow 0+3y=6 \\\ & \Rightarrow 3y=6 \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow y=\dfrac{6}{3} \\\ & \Rightarrow y=2 \\\ \end{aligned}$
Now, consider the equation $x+3y=6$ when $y=0$,
$\begin{aligned} & \Rightarrow x+3\times 0=6 \\\ & \Rightarrow x+0=6 \\\ & \Rightarrow x=6 \\\ \end{aligned}$
So, we got two points to plot the graph of the equation $x+3y=6$. Now we will get the table as follows:

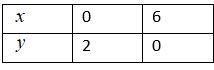
Next, consider the equation:
$2x-3y=12$
Now, we have to find two points to draw the graph of the equation.
For that take $x=0$, our equation,
$\begin{aligned} & \Rightarrow 2\times 0-3y=12 \\\ & \Rightarrow 0-3y=12 \\\ & \Rightarrow -3y=12 \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow y=\dfrac{12}{-3} \\\ & \Rightarrow y=-4 \\\ \end{aligned}$
Now, for $y=0$ we will obtain:
$\begin{aligned} & 2x-3\times 0=12 \\\ & \Rightarrow 2x-0=12 \\\ & \Rightarrow 2x=12 \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow x=\dfrac{12}{2} \\\ & \Rightarrow x=6 \\\ \end{aligned}$
Now, we can write the table for the above data. It is as follows:

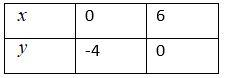
Now, we can plot the graph with the points (0, 2), (6, 0) and (0, -4), (6, 0).

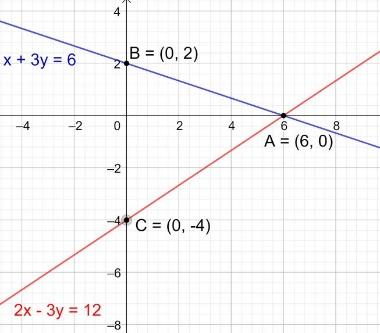
We can see that the lines represented by the equations $x+3y=6$ and $2x-3y=12$ meet the y-axis at B (0, 2) and C (0, -4) respectively.
Hence, the required coordinates are (0, 2) and (0, -4).

Note: Here, we can also check the coordinates by substituting it into any one of the equations. Since every point on the line is a solution of the equation, the point satisfies the equation if it lies on the line. Also, every solution of the equation is a point on the line. Otherwise, we can also find the points using the elimination method.