Question

Represent the complex number $z=1+i$ in polar form.

Answer 1

To convert a complex number into its polar form, we need to calculate the magnitude and the argument of the complex number. Magnitude is calculated by using the formula $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$. We know that the argument is the angle with the positive X-axis, and can be calculated using the formula $\theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$ .

Complete step by step solution:
We know that a complex number is mostly represented in one of the two forms, the standard form and the polar form. Any complex number in standard form is represented as $z=x+iy$ , where x and y are real numbers and $i=\sqrt{-1}$ . We also understand any complex number in the form $z=r\cos \theta +ir\sin \theta$ is said to be in polar form, and the polar coordinates are $\left( r,\theta \right)$ .
Let us assume a complex point P which represents $z=x+iy$ in the Cartesian plane. To convert this complex number into the polar form, we can see from the following figure, that r is the magnitude of this point P.

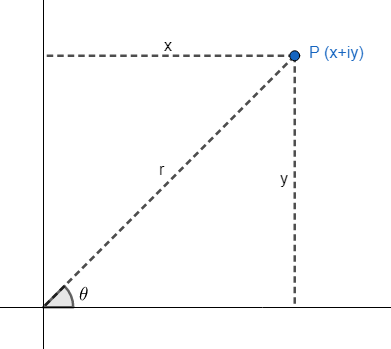
We know that the magnitude of the complex number z will be $\sqrt{{{x}^{2}}+{{y}^{2}}}$ .
Thus, we have, $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ .
We can also see in the figure that $\theta$ is the angle between the magnitude and the X-axis.
Thus, $\tan \theta =\dfrac{y}{x}$ .
Or, $\theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$ .
In our problem, we have $z=1+i$ .
So, we have $x=1\text{ and }y=1$ .
Using these values to calculate the magnitude, we get
$r=\sqrt{{{1}^{2}}+{{1}^{2}}}$
$\Rightarrow r=\sqrt{2}...\left( i \right)$
We can also use the values of x and y to calculate the argument of this complex number.
$\theta ={{\tan }^{-1}}\left( \dfrac{1}{1} \right)$
$\Rightarrow \theta ={{\tan }^{-1}}\left( 1 \right)$
$\Rightarrow \theta ={{45}^{\circ }}...\left( ii \right)$
Now, we can use the values from equation (i) and equation (ii) to convert this complex number into polar form.
$z=r\cos \theta +ir\sin \theta$
$\Rightarrow z=\sqrt{2}\cos \left( {{45}^{\circ }} \right)+i\sqrt{2}\sin \left( {{45}^{\circ }} \right)$
Thus, the polar form of the complex number $z=1+i\text{ is }z=\sqrt{2}\left[ \cos \left( {{45}^{\circ }} \right)+i\sin \left( {{45}^{\circ }} \right) \right]$ .

Note: We must not confuse between the Polar form and the Euler’s form of representation for a complex number. We must also take care that the argument is always calculated with respect to the positive X-axis, and that it is positive for anti-clockwise, and negative for clockwise rotation.