Question
Question: Represent that the motion of a bob of a pendulum with small amplitude is a linear simple harmonic mo...
Represent that the motion of a bob of a pendulum with small amplitude is a linear simple harmonic motion. And therefore obtain an expression for its period. What are the factors on which the period of this pendulum depends upon?
Solution
In the displaced position, there are two forces which are acting on the bob. One is gravitational force or the weight(mg) in the downward direction. The force is found by taking the product of the mass and the acceleration. The negative sign in the equation of force represents that the force and the angular displacement are found to be oppositely directed. This will help you in answering this question.
Complete answer:
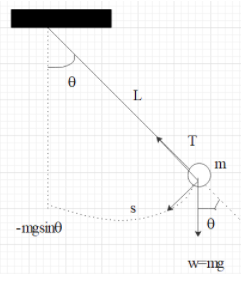
to represent the motion of the bob of the simple pendulum as simple harmonic motion. Consider a simple pendulum of mass mand the length L.
L=l+r
Where l be the length of the string and r be the radius of the bob.
Let us assume that OA be the initial position of the pendulum and OB, be its instantaneous position when the string makes an angle θ with the vertical.
In the displaced position, there are two forces which are acting on the bob. One is gravitational force or the weight(mg) in the downward direction. The second one is the tension T in the string. Third one is the weight mg which can be resolved into two rectangular components. The radial component mgcosθ along OB and the tangential component mgsinθ orthogonal to OB and directed towards the mean position.
Here we can see that mgcosθ is balanced by tension T in the string. And the component mgsinθ will provide the restoring force.
∴F=mgsinθ
Where the negative sign represents that the force and the angular displacement are found to be oppositely directed. Therefore the restoring force will be proportional to sinθ instead of θ. Therefore the net motion will not be simple harmonic.
If the angle is very small, we can write that,
sinθ≈θ=Lx
Therefore the force will become,
∴F=−mgLx⇒mF=L−gx
As we all know the force is found by taking the product of the mass and the acceleration, we can write that,
mma=L−gx∴a=L−gx........(1)
From this we will get that,
a∝−x∵Lg=constant
Hence, the motion of the bob of a simple pendulum will be simple harmonic.
The time period can be formulated as,
In S.H.M
a=−ω2x.............(2)
Comparing equation 1 and 2 will give,
ω2=Lg
As we all know the angular velocity can be shown as,
ω=T2π
Substituting this in the equation will give,
(T2π)2=Lg⇒T2π=Lg∴T=2πgL
Therefore the final equation for time period has been obtained. The period of a simple pendulum is dependent on the length of the pendulum and acceleration due to gravity. Hence the answer for the question has been calculated.
Note:
In physics especially in mechanics, simple harmonic motion is a special form of periodic motion in which the restoring force on the moving body will be directly proportional to the magnitude of the displacement of the body and acts towards the equilibrium position of the object.
