Question

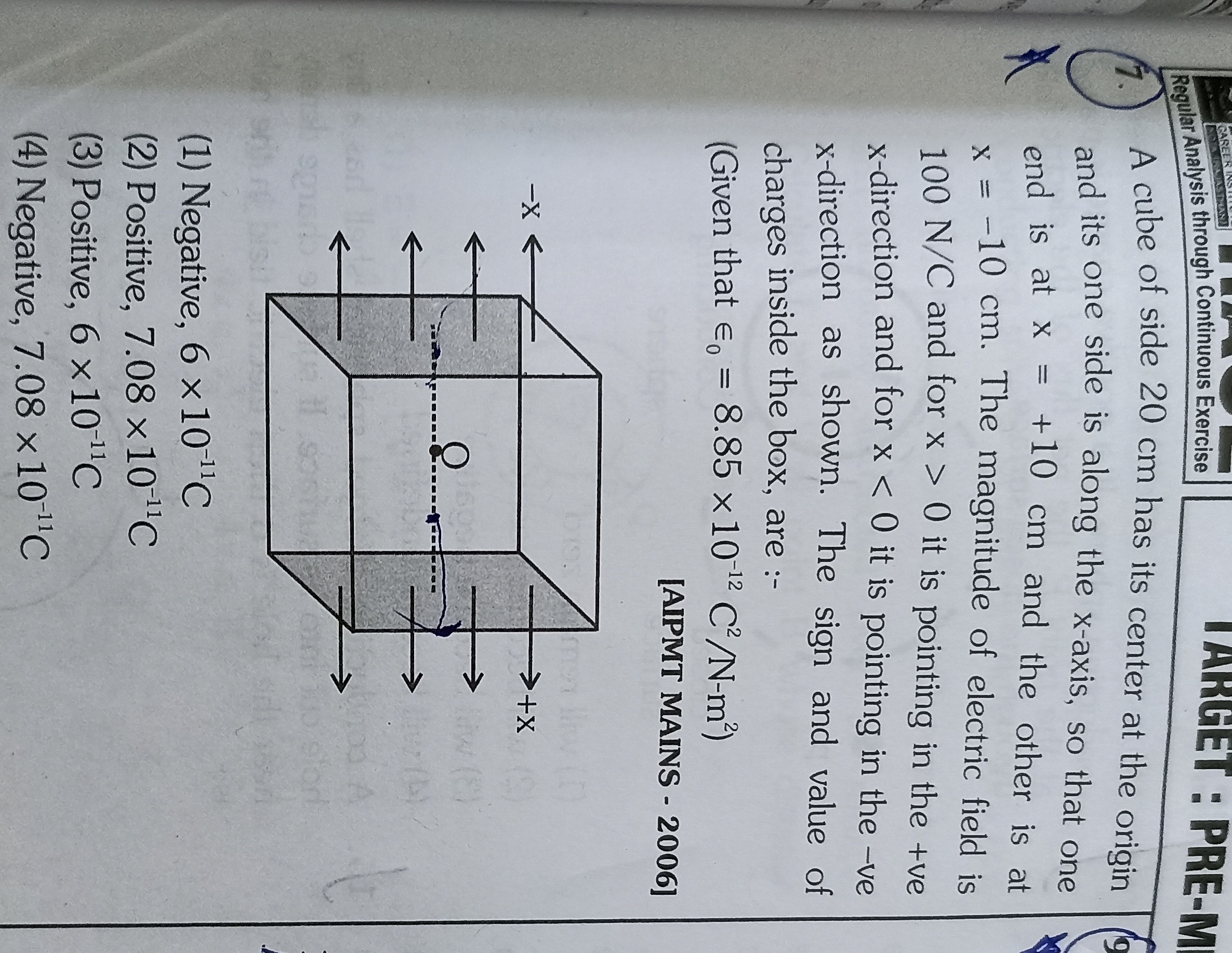
A cube of side 20 cm has its center at the origin and its one side is along the x-axis, so that one end is at x = +10 cm and the other is at x = -10 cm. The magnitude of electric field is 100 N/C and for x > 0 it is pointing in the +ve x-direction and for x < 0 it is pointing in the -ve x-direction as shown. The sign and value of charges inside the box, are :- (Given that $\epsilon_0$ = 8.85 x $10^{-12}$ $C^2$/N-$m^2$)

• A. Negative, 6 x $10^{-11}$C
• B. Positive, 7.08 × $10^{-11}$C
• C. Positive, 6 x $10^{-11}$C
• D. Negative, 7.08 ×$10^{-11}$C

Answer 1

Answer: (D)

(4) Negative, $7.08 \times 10^{-11}$C

Answer 2

The problem asks us to find the sign and value of the charge inside a cube using Gauss's Law.

1. Understand the Geometry and Electric Field:

• The cube has a side length $L = 20 \, \text{cm} = 0.2 \, \text{m}$.

• Its center is at the origin, so its faces are at $x = \pm 10 \, \text{cm}$, $y = \pm 10 \, \text{cm}$, and $z = \pm 10 \, \text{cm}$.

• The magnitude of the electric field is $E = 100 \, \text{N/C}$.

• The problem states: "for x > 0 it is pointing in the +ve x-direction and for x < 0 it is pointing in the -ve x-direction as shown." However, observing the diagram:

  • For the face at $x = +10 \, \text{cm}$ (where $x > 0$), the arrows are pointing inward (towards the -x direction).
  • For the face at $x = -10 \, \text{cm}$ (where $x < 0$), the arrows are pointing outward (towards the +x direction).

  This indicates a contradiction between the textual description of the field direction and the visual representation in the diagram. Given the phrase "as shown", it is typically implied that the diagram provides the definitive visual information. The field lines shown in the diagram (inward for $x>0$, outward for $x<0$) are consistent with the electric field of a negative point charge at the origin (field lines point towards a negative charge). Therefore, we will interpret the electric field direction as shown in the diagram:

  • For $x > 0$, $\vec{E} = -100 \, \hat{i} \, \text{N/C}$.
  • For $x < 0$, $\vec{E} = +100 \, \hat{i} \, \text{N/C}$.

2. Calculate the Area of the Faces:

The area of each face of the cube is $A = L^2 = (0.2 \, \text{m})^2 = 0.04 \, \text{m}^2$.

3. Calculate the Electric Flux through Each Face:

Gauss's Law states $\Phi_E = \oint \vec{E} \cdot d\vec{A}$. The total flux is the sum of fluxes through all six faces.

• Flux through the right face (at $x = +0.1 \, \text{m}$):

  The electric field is $\vec{E}_R = -100 \, \hat{i}$. The outward area vector for this face is $\vec{A}_R = A \, \hat{i} = 0.04 \, \hat{i} \, \text{m}^2$. $\Phi_R = \vec{E}_R \cdot \vec{A}_R = (-100 \, \hat{i}) \cdot (0.04 \, \hat{i}) = -100 \times 0.04 = -4 \, \text{N m}^2/\text{C}$.

• Flux through the left face (at $x = -0.1 \, \text{m}$):

  The electric field is $\vec{E}_L = +100 \, \hat{i}$. The outward area vector for this face is $\vec{A}_L = -A \, \hat{i} = -0.04 \, \hat{i} \, \text{m}^2$. $\Phi_L = \vec{E}_L \cdot \vec{A}_L = (100 \, \hat{i}) \cdot (-0.04 \, \hat{i}) = -100 \times 0.04 = -4 \, \text{N m}^2/\text{C}$.

• Flux through the other four faces (top, bottom, front, back):

  For these faces (at $y = \pm 0.1 \, \text{m}$ and $z = \pm 0.1 \, \text{m}$), their outward area vectors are perpendicular to the x-axis (e.g., $\hat{j}$, $-\hat{j}$, $\hat{k}$, $-\hat{k}$). Since the electric field is purely along the x-axis, the dot product $\vec{E} \cdot \vec{A}$ will be zero for these faces. $\Phi_{other} = 0$.

4. Calculate the Total Electric Flux:

The total flux through the cube is the sum of fluxes through all faces: $\Phi_{total} = \Phi_R + \Phi_L + \Phi_{other} = (-4) + (-4) + 0 = -8 \, \text{N m}^2/\text{C}$.

5. Apply Gauss's Law to Find the Enclosed Charge:

According to Gauss's Law, $\Phi_{total} = \frac{Q_{enc}}{\epsilon_0}$, where $Q_{enc}$ is the charge enclosed within the cube and $\epsilon_0$ is the permittivity of free space. Given $\epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/(\text{N m}^2)$.

$Q_{enc} = \Phi_{total} \times \epsilon_0$

$Q_{enc} = (-8 \, \text{N m}^2/\text{C}) \times (8.85 \times 10^{-12} \, \text{C}^2/(\text{N m}^2))$

$Q_{enc} = -70.8 \times 10^{-12} \, \text{C}$

$Q_{enc} = -7.08 \times 10^{-11} \, \text{C}$.

6. Determine the Sign and Value:

The calculated charge is negative, and its value is $7.08 \times 10^{-11}$ C.

The final answer is (4).

Explanation of the solution:

Gauss's Law is applied to the cubic Gaussian surface. The electric field directions are taken from the diagram as indicated by "as shown", which shows field lines converging towards the center. The flux is calculated for each face: the right face at $x=+0.1$ m has $\vec{E} = -100\hat{i}$ and $\vec{A} = A\hat{i}$, giving negative flux. The left face at $x=-0.1$ m has $\vec{E} = +100\hat{i}$ and $\vec{A} = -A\hat{i}$, also giving negative flux. Flux through other faces is zero as $\vec{E}$ is perpendicular to their area vectors. The total flux is the sum of these, resulting in a negative value. Using Gauss's Law ($\Phi = Q_{enc}/\epsilon_0$), a negative total flux implies a negative enclosed charge.