Solveeit Logo
Login

Question

Question: Reflection of the point \(\left( \alpha ,\beta ,\gamma \right)\) in the XY plane is: a). \(\left( ...

Reflection of the point (α,β,γ)\left( \alpha ,\beta ,\gamma \right) in the XY plane is:
a). (−α,β,γ)\left( -\alpha ,\beta ,\gamma \right)
b). (α,β,0)\left( \alpha ,\beta ,0 \right)
c). (0,0,γ)\left( 0,0,\gamma \right)
d). (α,β,−γ)\left( \alpha ,\beta ,-\gamma \right)

Explanation

Solution

We will use the concept of 3-D geometry to find the reflection of point (α,β,γ)\left( \alpha ,\beta ,\gamma \right)in the XY plane. We will use the concept that when we take the reflection of any point in the XY plane then the x and y coordinate of the point remains the same and z-coordinate changes only in sign but magnitude remains the same.

Complete step-by-step solution:
From the question we can see that (α,β,γ)\left( \alpha ,\beta ,\gamma \right) is a point which lies in the 3-D plane. Since, we have to find the reflection of point (α,β,γ)\left( \alpha ,\beta ,\gamma \right)in the XY plane.
Let us assume that ADCB is an XY plane and point E (α,β,γ)\left( \alpha,\beta,\gamma \right) be the point that lies above the plane XY.

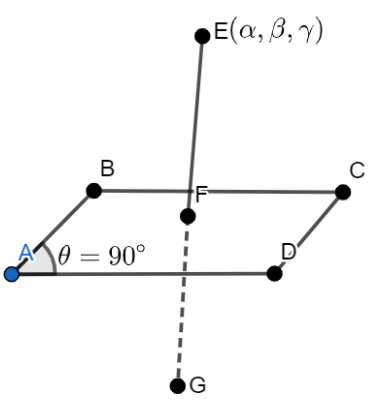
Let us say that AD is the x-axis and AB is the y-axis and AD is perpendicular to AB.
So, the distance of point E from the x-axis is α\alpha , and the distance of point E from the y-axis is β\beta and that from the z-axis is γ\gamma .
Now, when we take the reflection of point E in the XY plane ADCB then we will get point G.
So, we can say that we have to move the same distance α\alpha on the x-axis(i.e. on line AD) and on the y-axis, we will also move the same β\beta distance but since G is opposite to E so we have to move in an opposite direction on the z-axis to reach point G but its magnitude is same as that of γ\gamma .
So, we can say that the point G is (α,β,−γ)\left( \alpha ,\beta ,-\gamma \right).
Hence, option(d) is the correct answer.

Note: Students are required to note that when we take the reflection of any point about XY then only the sign of z-coordinate changes and the rest of the coordinates remains the same. Similarly, when we take a reflection of point about YZ axis then the sign of only x-coordinate changes and the rest of things remains the same. Similarly, when we take a reflection of point about XZ axis then sign of y-coordinates changes only, and remaining coordinates remain the same as it is before.