Question
Question: Refer to the circuit shown. What will be the total power dissipation in the circuit if \[P\] is the ...
Refer to the circuit shown. What will be the total power dissipation in the circuit if P is the power dissipated in R1 ? It is given that R2=4R1 and R3=12R1
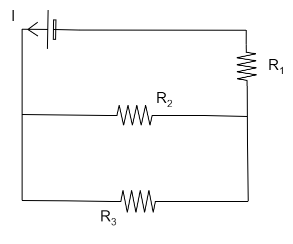
Solution
We are asked to find the power dissipation in the given circuit of given current and resistances. We start by finding the equivalent of the three resistances. Two of them are in parallel and the other is in series with the equivalent of the parallel resistors. After this, the answer can be found out pretty quickly as the formula is very direct. After the value of total power dissipation is found, the relation between it and the given power can be found out, giving us the solution.
Formulas used:
The value of equivalent resistance of two resistors in parallel connection is given by,
Rp=R1+R2R1R2
The value of equivalent resistance of two resistors in series connection is given by,
RS=R1+R2
Where R1 and R2 are resistances of the individual resistors.
The total power in a circuit can be found out as,
P=I2R
Where I is the current through the circuit and R is the total resistance of the circuit.
Complete step by step answer:
Let us start by gathering the given information.
R2=4R1
⇒R3=12R1
The resistors R2 and R3 are in parallel, hence their equivalent resistance can be found out using,
