Question

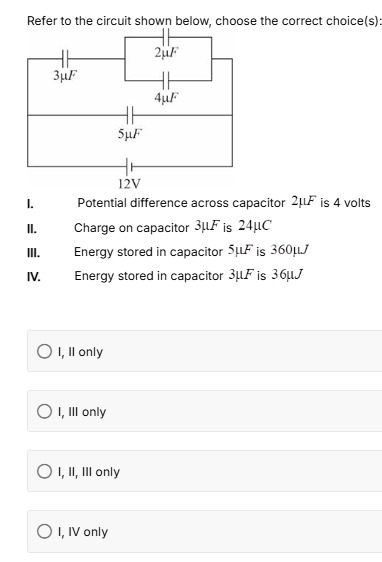
Refer to the circuit shown below, choose the correct choice(s):

I. Potential difference across capacitor 2$\mu F$ is 4 volts II. Charge on capacitor 3$\mu F$ is 24$\mu C$ III. Energy stored in capacitor 5$\mu F$ is 360$\mu J$ IV. Energy stored in capacitor 3$\mu F$ is 36$\mu J$

• A. I, II only
• B. I, III only
• C. I, II, III only
• D. I, IV only

Answer 1

Answer: (C)

I, II, III only

Answer 2

To solve this problem, we need to analyze the given circuit diagram step-by-step to find the equivalent capacitance, charges, voltages, and energies for each capacitor.

Circuit Analysis:

1. Identify Parallel and Series Combinations:

   • The 2µF and 4µF capacitors are connected in parallel. Their equivalent capacitance, $C_{p1}$, is: $C_{p1} = 2\mu F + 4\mu F = 6\mu F$

   • This parallel combination ($C_{p1}$) is connected in series with the 3µF capacitor. Their equivalent capacitance, $C_{s1}$, is: $\frac{1}{C_{s1}} = \frac{1}{C_{p1}} + \frac{1}{3\mu F} = \frac{1}{6\mu F} + \frac{1}{3\mu F} = \frac{1+2}{6\mu F} = \frac{3}{6\mu F} = \frac{1}{2\mu F}$ $C_{s1} = 2\mu F$

   • The entire branch ($C_{s1}$) is connected in parallel with the 5µF capacitor. The total equivalent capacitance of the circuit, $C_{eq}$, is: $C_{eq} = C_{s1} + 5\mu F = 2\mu F + 5\mu F = 7\mu F$

2. Calculate Total Charge and Voltage Distribution:

   • The total voltage supplied by the battery is $V_{total} = 12V$.
   • Since the 5µF capacitor is in parallel with the rest of the circuit (the $C_{s1}$ branch), the voltage across the 5µF capacitor is $V_{5\mu F} = 12V$.
   • The voltage across the $C_{s1}$ branch (which contains the 3µF capacitor and the 2µF || 4µF combination) is also $V_{s1} = 12V$.

Now let's evaluate each statement:

I. Potential difference across capacitor 2µF is 4 volts.

• The charge on the series branch ($C_{s1}$) is $Q_{s1} = C_{s1} \times V_{s1} = 2\mu F \times 12V = 24\mu C$.
• Since the 3µF capacitor is in series with the parallel combination of 2µF and 4µF (represented by $C_{p1}$), the charge on the 3µF capacitor is $Q_{3\mu F} = Q_{s1} = 24\mu C$.
• The charge on the parallel combination ($C_{p1}$) is also $Q_{p1} = Q_{s1} = 24\mu C$.
• The potential difference across the parallel combination ($C_{p1}$) is $V_{p1} = \frac{Q_{p1}}{C_{p1}} = \frac{24\mu C}{6\mu F} = 4V$.
• Since the 2µF and 4µF capacitors are in parallel, the potential difference across each of them is the same as $V_{p1}$. Therefore, the potential difference across the 2µF capacitor is $V_{2\mu F} = 4V$. Statement I is correct.

II. Charge on capacitor 3µF is 24µC.

• As calculated above, the charge on the 3µF capacitor is $Q_{3\mu F} = 24\mu C$. Statement II is correct.

III. Energy stored in capacitor 5µF is 360µJ.

• The voltage across the 5µF capacitor is $V_{5\mu F} = 12V$.
• The energy stored in a capacitor is given by $U = \frac{1}{2}CV^2$.
• $U_{5\mu F} = \frac{1}{2} \times (5\mu F) \times (12V)^2 = \frac{1}{2} \times 5 \times 10^{-6} F \times 144 V^2 = 5 \times 72 \mu J = 360 \mu J$. Statement III is correct.

IV. Energy stored in capacitor 3µF is 36µJ.

• The charge on the 3µF capacitor is $Q_{3\mu F} = 24\mu C$.
• The potential difference across the 3µF capacitor is $V_{3\mu F} = \frac{Q_{3\mu F}}{C_{3\mu F}} = \frac{24\mu C}{3\mu F} = 8V$.
• The energy stored in the 3µF capacitor is $U_{3\mu F} = \frac{1}{2}C_{3\mu F}V_{3\mu F}^2 = \frac{1}{2} \times (3\mu F) \times (8V)^2 = \frac{1}{2} \times 3 \times 10^{-6} F \times 64 V^2 = 3 \times 32 \mu J = 96 \mu J$. Statement IV is incorrect.

Conclusion: Statements I, II, and III are correct.