Question

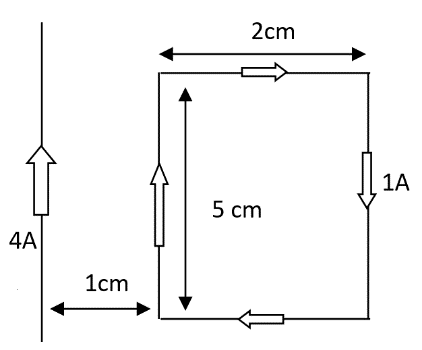
Rectangular loop of wire of size 2cm $\times$ 5 cm carries a Steady Current of 1 ampere. A straight long wire carrying 4-ampere current is kept near the loop as shown in the figure. If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current-carrying wire.

Answer 1

Hint: Use the formula for the torque acting on the current loop and check the angle between the perpendicular of the loop and magnetic field due to current-carrying wire. For the force acting on the loop use the formula F = BiL

Complete step-by-step answer:
Torque on the current loop is given by $\tau = NIA \times B = NIAB\sin \theta$
The angle between the perpendicular of the loop and magnetic field due to the current-carrying wire is zero.
So the torque acting on the current loop is zero.
We know the force acting on the current-carrying wire due to the magnetic field is given by:
$F_B = i(l \times B)$
On the line, AB and CD's magnetic forces are equal and opposite. So they cancel out each other.
Magnetic force on the line AD is
$F = BiL$
$B = \dfrac{\mu_o I}{2\pi r }$ where I is the current in the wire
$F =\dfrac{\mu i L }{2\pi r}$ (attractive)
Magnetic force on the line BC is
$B^{I} = \dfrac{\mu_o I }{2\pi r_2}$
So $F_{BC} = B^I I L = \dfrac{\mu i I L}{2\pi r_2}$ (repulsive)
Current is opposite two branches we get the net force acting is equal to
The net force is $F_{net} = F – F^I$
$F_{net} = \dfrac{\mu_o i I L }{2\pi} (\dfrac{1}{r} – \dfrac{1}{r_2} )$
Now we have i = 4 A , I = 1 A, r = 1 cm $r_2$ = 3 cm, L = 5 cm
So we get the value of the net force as : $F_n = 2 \times 10^{-7} \times 4 \times 1 \times 0.05(\dfrac{1}{0.01} - \dfrac{1}{0.03} ) = 26.66 \times 10^{-7} N$
So using the expression for magnetic force acting on a current-carrying wire due to magnetic field be obtained net force acting on the current loop as: $26.66 \times 10^{-7}$ N

Note: One of the common mistakes that we tend to make in this kind of problem while finding the torque is that we take the angle theta angle between the plane of the current loop and magnetic field which is wrong. We need to understand here that theta is the angle between the perpendicular of the loop and the magnetic field inside the loop.