Solveeit Logo
Login

Question

Question: Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 c...

Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 cm. Find (i) the moment of inertia of the system about an axis joining two of the particles and (ii) moment of inertia of the system about an axis passing through one of the particles and perpendicular to the plane of the particles respectively :-

A

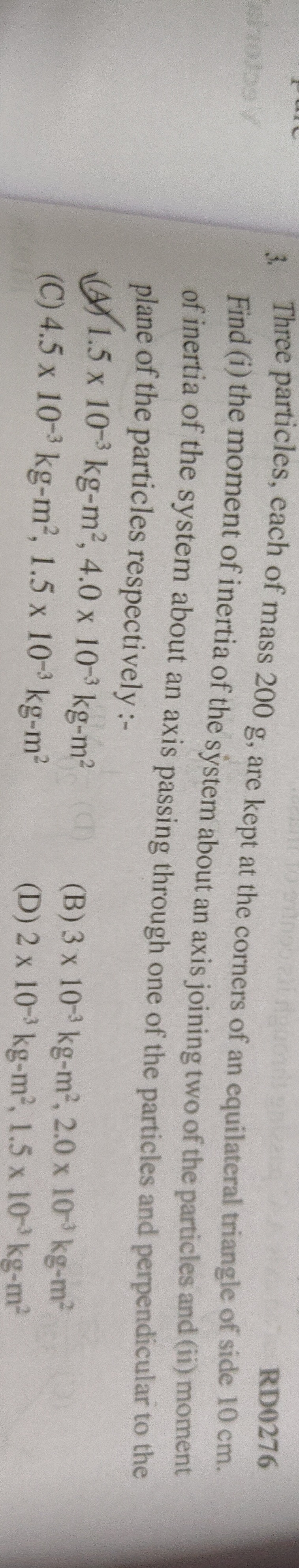
1.5 x 10^{-3} kg-m², 4.0 x 10^{-3} kg-m²

B

3 x 10^{-3} kg-m², 2.0 x 10^{-3} kg-m²

C

4.5 x 10^{-3} kg-m², 1.5 x 10^{-3} kg-m²

D

2 x 10^{-3} kg-m², 1.5 x 10^{-3} kg-m²

Answer

1.5 x 10^{-3} kg-m², 4.0 x 10^{-3} kg-m²

Explanation

Solution

1. Given Data:

  • Mass of each particle, m=200 g=0.2 kgm = 200 \text{ g} = 0.2 \text{ kg}
  • Side of the equilateral triangle, a=10 cm=0.1 ma = 10 \text{ cm} = 0.1 \text{ m}

2. Moment of Inertia (i) about an axis joining two of the particles:

Let the three particles be A, B, and C. We choose the axis to pass through particles B and C.

  • The perpendicular distance of particles B and C from this axis is zero. Hence, their contribution to the moment of inertia is zero.
  • The perpendicular distance of particle A from the axis BC is the altitude (hh) of the equilateral triangle. For an equilateral triangle of side aa, the altitude is h=32ah = \frac{\sqrt{3}}{2} a. h=32×0.1 m=0.053 mh = \frac{\sqrt{3}}{2} \times 0.1 \text{ m} = 0.05\sqrt{3} \text{ m}
  • The moment of inertia (I1I_1) about this axis is the sum of mr2m r^2 for each particle: I1=mAh2+mB(0)2+mC(0)2I_1 = m_A h^2 + m_B (0)^2 + m_C (0)^2 I1=mh2I_1 = m h^2 I1=0.2 kg×(0.053 m)2I_1 = 0.2 \text{ kg} \times (0.05\sqrt{3} \text{ m})^2 I1=0.2×(0.0025×3)I_1 = 0.2 \times (0.0025 \times 3) I1=0.2×0.0075I_1 = 0.2 \times 0.0075 I1=0.0015 kg-m2=1.5×10−3 kg-m2I_1 = 0.0015 \text{ kg-m}^2 = 1.5 \times 10^{-3} \text{ kg-m}^2

3. Moment of Inertia (ii) about an axis passing through one of the particles and perpendicular to the plane of the particles:

Let the axis pass through particle A and be perpendicular to the plane of the triangle.

  • The perpendicular distance of particle A from this axis is zero. Hence, its contribution to the moment of inertia is zero.
  • Particles B and C are at a distance aa (side length) from particle A. Since the axis is perpendicular to the plane, their perpendicular distances from the axis are aa.
  • The moment of inertia (I2I_2) about this axis is: I2=mA(0)2+mBa2+mCa2I_2 = m_A (0)^2 + m_B a^2 + m_C a^2 I2=0+ma2+ma2I_2 = 0 + m a^2 + m a^2 I2=2ma2I_2 = 2 m a^2 I2=2×0.2 kg×(0.1 m)2I_2 = 2 \times 0.2 \text{ kg} \times (0.1 \text{ m})^2 I2=0.4×0.01I_2 = 0.4 \times 0.01 I2=0.004 kg-m2=4.0×10−3 kg-m2I_2 = 0.004 \text{ kg-m}^2 = 4.0 \times 10^{-3} \text{ kg-m}^2

Conclusion:

The moment of inertia for case (i) is 1.5×10−3 kg-m21.5 \times 10^{-3} \text{ kg-m}^2 and for case (ii) is 4.0×10−3 kg-m24.0 \times 10^{-3} \text{ kg-m}^2.